ABCDE is a regular pentagon and a rectangle AXYE is drawn on the side AE such that the vertices X and Y lie on the sides BC and CD respectively. Calculate the size of
(i) an interior angle of the pentagon ;
(ii) < BXA.
Explanation
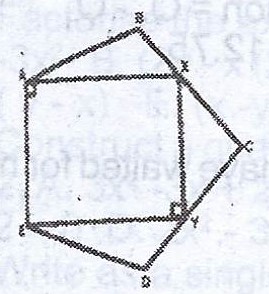
(i) Sum of interior angles of a regular polygon = \((2n - 4) \times 90°\)
For a pentagon, \((2(5) - 4) \times 90° = 6 \times 90° = 540°\)
Interior angle = \(\frac{540°}{5} = 108°\)
(ii) < BXA = 108° - 90° = 18°
< ABX = 108° (as shown above)
\(\therefore < BXA = 180° - (108° + 18°) = 54°\)

