(a) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.
(b) 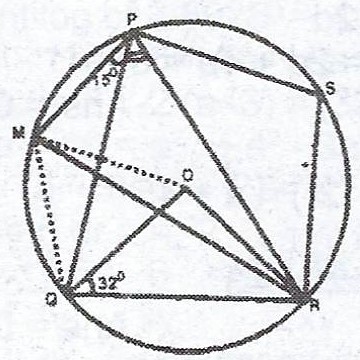
In the diagram, O is the centre of the circle, < OQR = 32° and < MPQ = 15°. Calculate (i) < QPR ; (ii) < MQO.
Explanation
(a) 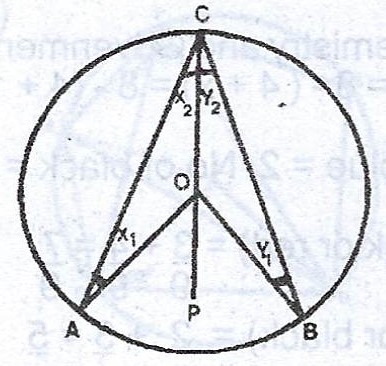
Given: Circle ABC with centre O
To prove : < AOB = 2 < ACB
Construction: Join CO produced to P.
Proof: With lettering as in the figure,
OA = OB (radii) ; \(x_{1} = x_{2}\) (base angles of an isosceles triangle)
\(\therefore < AOP = x_{1} + x_{2}\) (exterior angle of triangle AOC)
\(\therefore < AOP = 2x_{2} (x_{1} = x_{2})\)
Also, \(< BOP = 2y_{2}\) (similar proof as the earlier done ones)
\(\therefore < AOB = 2x_{2} + 2y_{2} = 2(x_{2} + y_{2})\)
\(< AOB = 2 \times < ABC\) (proven)
(b) From the diagram, < OQR = 32° and < MPQ = 15°.
(i) \(\therefore < ORQ = 32°\) (base angles of an isosceles triangle)
\(< OQR = 180° - (32° + 32°) = 180° - 64° = 116°\)
\(\therefore < QPR = \frac{116°}{2} = 58°\) (angle subtended at the centre)
(ii) Join MO and MQ,
Since < MPQ = 15°
then < MOQ = 2 < MPQ (angle at the centre)
\(\therefore < MOQ = 2 \times 15° = 30°\)
\(\therefore < OMQ = < MQO \) (base angles of an isosceles triangle)
\(\therefore < MQO = \frac{180° - 30°}{2} = 75°\)

