From a horizontal distance of 8.5 km, a pilot observes that the angles of depression of the top and the base of a control tower are 30° and 33° respectively. Calculate, correct to three significant figures :
(a) the shortest distance between the pilot and the base of the control tower;
(b) the height of the control tower.
Explanation
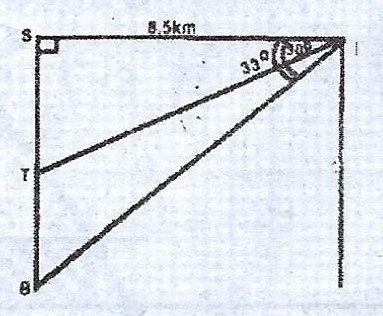
Let T and B be the top and base of the control tower respectively; P, the point of pilot's observation and PS, the line of observation.
(a) Shortest distance is |PB|.
\(\therefore \cos 33° = \frac{8.5}{PB}\)
\(PB = \frac{8.5}{\cos 33} = \frac{8.5}{0.8387}\)
\(|PB| = 10.135km \approxeq 10.1km\)
(b) Height of the control tower = |SB| - |ST|
\(\therefore \tan 33° = \frac{|SB|}{8.5 km} \implies |SB| = 8.5 \tan 33°\)
\(|SB| = 5.52 km\)
\(\tan 30° = \frac{|ST|}{8.5 km} \implies |ST| = 8.5 \tan 30°\)
\(|ST| = 4.907 km\)
\(\therefore\) The height of the tower = 5.52 km - 4.907 km = 0.613 km.

