The table below shows the weekly profit in naira from a mini-market.
| Weekly profit (N) | 1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 |
| Freq | 6 | 6 | 12 | 11 | 10 | 5 |
(a) Draw the cumulative frequency curve of the data;
(b) From your graph, estimate the : (i) median ; (ii) 80th percentile
(c) What is the modal weekly profit?
Three towns P, Q and R are such that the distance between P and Q is 50km and the distance between P and R is 90km. If the bearing of Q from P is 075° and the bearing of R from P is 310°, find the :
(a) distance between Q and R ;
(b) baering of R from Q.
(a) The distribution of junior workers in an institution is as follows: Clerks – 78, Drivers – 36, Typists – 44, Messengers – 52, Others – 30. Represent the above information by a pie chart.
(b) The table below shows the frequency distribution of marks scored by 30 candidates in an aptitude test.
| Marks | 4 | 5 | 6 | 7 | 8 | 9 |
| No of candidates | 5 | 8 | 5 | 6 | 4 | 2 |
Find the mean score to the nearest whole number.
(a) Copy and complete the following table for the relation \(y = \frac{5}{2} + x – 4x^{2}\)
| x | -2.0 | -1.5 | -1.0 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2.0 |
| y | -15.5 | 1 | 2.5 |
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, draw the graph of the relation for \(-2.0 \leq x \leq 2.0\).
(c) What is the maximum value of y?
(d) From your graph, obtain the roots of the equation \(8x^{2} – 2x – 5 = 0\)
(a) 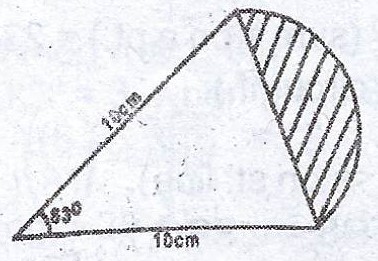
Calculate the area of the shaded segment of the circle shown in the diagram [Take \(\pi = \frac{22}{7}\)]
(b) A tin has radius 3cm and height 6cm. Find the (i) total surface area of the tin ; (ii) volume, in litres, that will fill the tin to capacity, correct to two decimal places.
[Take \(\pi = \frac{22}{7}\)]
(a) Using a ruler and a pair of compasses only, construct: (i) a triangle ABC such that |AB| = 5cm, |AC| = 7.5cm and < CAB = 120°; (ii) the locus \(l_{1}\) of points equidistant from A and B; (iii) the locus \(l_{2}\) of points equidistant from AB and AC which passes through triangle ABC .
(b) Label the point P where \(l_{1}\) and \(l_{2}\) intersect.
(c) Measure |CP|.
(a) If \(17x = 375^{2} – 356^{2}\), find the exact value of x.
(b) If \(4^{x} = 2^{\frac{1}{2}} \times 8\), find x.
(c) The sum of the first 9 terms of an A.P is 72 and the sum of the next 4 terms is 71, find the A.P.
(a) In a game, a fair die is rolled once and two unbiased coins are tossed at once. What is the probability of obtaining 3 and a tail?
(b) A box contains 10 marbles, 7 of which are black and 3 are red. Two marbles are drawn one after the other without replacement. Find the probability of getting:
(i) a red, then a black marble ; (ii) two black marbles.
(a) The sides PQ and PR of \(\Delta\) PQR are produced to T and S respectively, such that TQR = 131° and < QRS = 98°. Find < QPR.
(b) The circumference of a circular track is 400m. Find its radius, correct to the nearest metre. [Take \(\pi = \frac{22}{7}\)]
(a) The angle of a sector of a circle radius 7cm is 108°. Calculate the perimeter of the sector. [Take \(\pi = \frac{22}{7}\)]
(b) A boat is on the same horizontal level as the foot of a cliff, and the angle of depression of the boat from the top of the cliff is 30°. If the boat is 120m away from the foot of the cliff, find the height of the cliff correct to three significant figures.
(a) Solve the following pair of simultaneous equations: \(2x + 5y = 6\frac{1}{2} ; 5x – 2y = 9\)
(b) If \(\log_{10} (2x + 1) – \log_{10} (3x – 2) = 1\), find x.
(a) If \(9^{2x – 1} = \frac{81^{x – 2}}{3^{x}}\), find x.
(b) Without using Mathematical Tables, evaluate: \(\sqrt{\frac{0.81 \times 10^{-5}}{2.25 \times 10^{7}}}\)
The data below shows the number of worker?
employed in the various sections of a construction
company in Lagos.
Carpenters 24 Labourers 27
Plumbers 12 Plasterers 15
Painters 9 Messengers 3
Bricklayers 18
If a worker is retrenched, what is the probability that he is a plumber or plasterer.
- A. 1/27
- B. 1/9
- C. 5/36
- D. 1/4
- E. 3/4
The data below shows the number of worker?
employed in the various sections of a construction
company in Lagos.
Carpenters 24 Labourers 27
Plumbers 12 Plasterers 15
Painters 9 Messengers 3
Bricklayers 18
If one of the workers is absent on a certain day,
what is the probability that he is a bricklayer?
- A. 1/12
- B. 1/9
- C. 2/9
- D. 1/6
- E. 1/4
A fair die is rolled once. What is the probability of
obtaining 4 or 6?
- A. 1/12
- B. 1/6
- C. 1/3
- D. 1/2
- E. 2/3
What is the probability of throwing a number greater than 2 with a single fair die
- A. 1/6
- B. 1/3
- C. 1/2
- D. 2/3
- E. 5/6
A number is chosen at random from the set (1 ,2,3
….,9, 10). What is the probability that the number
is greater than or equal to 7?
- A. 1/10
- B. 3/10
- C. 2/5
- D. 3/5
- E. 7/10
| Marks | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No of students | 1 | 3 | 2 | 0 | 1 | 6 | 1 | 0 | 1 | 0 |
The table above shows the scores of 15 students in a Physics test.
How many students scored at least 5?
- A. 1
- B. 6
- C. 8
- D. 9
- E. 14
A group of students measured a certain angle
(to the nearest degree) and obtained the following
results: 75o, 76o, 72o, 73o, 74o, 79o, 72o, 72o, 77o,
72o, 71o, 70o, 78o, 73o. Find the mode
- A. 79o
- B. 78o
- C. 74o
- D. 73o
- E. 72o

The data below shows the frequency distribution
of marks scored by a group of students in a class
test.
Find the mean mark.
- A. 1
- B. 1.3
- C. 2
- D. 3
- E. 3.8

The data below shows the frequency distribution
of marks scored by a group of students in a class
test.
What is the modal score
- A. 2
- B. 3
- C. 4
- D. 5
- E. 6


