(a) The angle of a sector of a circle radius 7cm is 108°. Calculate the perimeter of the sector. [Take \(\pi = \frac{22}{7}\)]
(b) A boat is on the same horizontal level as the foot of a cliff, and the angle of depression of the boat from the top of the cliff is 30°. If the boat is 120m away from the foot of the cliff, find the height of the cliff correct to three significant figures.
Explanation
(a) 
Length of arc AB = \(\frac{108°}{360°} \times 2 \times \frac{22}{7} \times 7 = \frac{132}{10} =13.2cm\)
Perimeter of the sector = \(13.2cm + 7cm + 7cm = 27.2cm\)
(b) 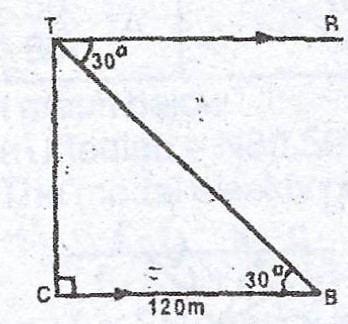
Let T = top of cliff, C = bottom of cliff, B = the boat.
Since angle of depression = 30°
then < CBT = 30° (alternate angles TR//CB)
\(\therefore \text{Height of the cliff} (CT) = 120 \times 0.5774m\)
= \(69.288m \approxeq 69.3m\)

