(a) 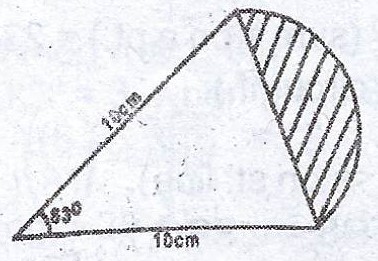
Calculate the area of the shaded segment of the circle shown in the diagram [Take \(\pi = \frac{22}{7}\)]
(b) A tin has radius 3cm and height 6cm. Find the (i) total surface area of the tin ; (ii) volume, in litres, that will fill the tin to capacity, correct to two decimal places.
[Take \(\pi = \frac{22}{7}\)]
Explanation
(a) Area of the shaded segment = Area of sector - Area of triangle
= \(\frac{\theta}{360°} \times \pi r^{2} - \frac{1}{2} ab \sin \theta\)
Area of sector = \(\frac{63}{360} \times \frac{22}{7} \times 10^{2}\)
= \(55 cm^{2}\)
Area of triangle = \(\frac{1}{2} \times 10 \times 10 \times \sin 63°\)
= \(50 \times 0.891 = 44.55 cm^{2}\)
\(\therefore \text{Area of the shaded segment} = 55 - 44.55 = 10.45 cm^{2}\)
(b) (i) Total surface area = \(2\pi r (r + h)\)
= \(2 \times \frac{22}{7} \times 3 (3 + 6)\)
= \(\frac{132}{7} \times 9 = \frac{1188}{7}\)
= \(169.71 cm^{2}\)
(ii) Volume of tin = \(\pi r^{2} h\)
= \(\frac{22}{7} \times 3 \times 3 \times 6 = \frac{1188}{7}\)
\(\approxeq 169.71 cm^{3}\)

