P and Q are two points on latitude 55°N and their longitudes are 33°W and 20°E respectively. Calculate the distance between P and Q measured along
(a) the parallel of latitude ;
(b) a great circle.
[Take \(\pi = \frac{22}{7}\) and radius of the earth = 6400km].
The table below shows the frequency distribution of the marks scored by fifty students in an examination.
| Marks (%) | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 |
| Freq | 2 | 3 | 4 | 6 | 13 | 10 | 5 | 3 | 2 | 2 |
(a) Draw the cumulative frequency curve for the distribution.
(b) Use your curve to estimate the : (i) upper quartile; (ii) pass mark if 60% of the students passed.
(a) Copy and complete the following table of values for \(y = 3\sin 2\theta – \cos \theta\).
| \(\theta\) | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| y | -1.0 | 0 | 1.0 |
(b) Using a scale of 2cm to 30° on the \(\theta\) axis and 2cm to 1 unit on the y- axis, draw the graph of \(y = 3 \sin 2\theta – \cos \theta\) for \(0° \leq \theta \leq 180°\).
(c) Use your graph to find the : (i) solution of the equation \(3 \sin 2\theta – \cos \theta = 0\), correct to the nearest degree; (ii) maximum value of y, correct to one decimal place.
(a) What is the 25th term of 5, 9, 13,… ?
(b) Find the 5th term of \(\frac{8}{9}, \frac{-4}{3}, 2, …\).
(c) The 3rd and 6th terms of a G.P are \(48\) and \(14\frac{2}{9}\) respectively. Write down the first four terms of the G.P.
(a) Prove that the angle which an arc of a circle subtends at the centre is twice that which it subtends at any point on the remaining part of the circumference.
(b) 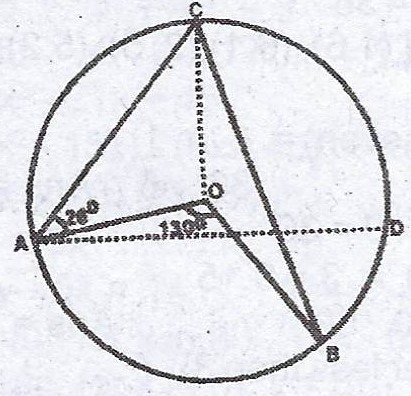
In the diagram, O is the centre of the circle ACDB. If < CAO = 26° and < AOB = 130°. Calculate : (i) < OBC ; (ii) < COB.
(a) 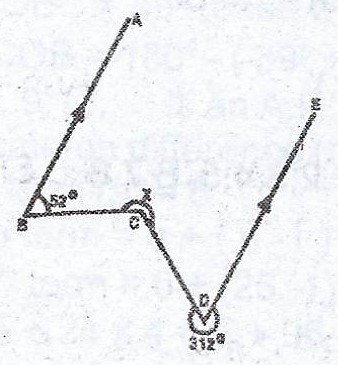
In the diagram, BA is parallel to DE. Find the value of x.
(b) Illustrate graphically and shade the region in which inequalities \(y – 2x < 5 ; 2y + x \geq 4 ; y + 2x \leq 10\) are satisfied.
(a)(i) Given that \(\log_{10} 5 = 0.699\) and \(\log_{10} 3 = 0.477\), find \(\log_{10} 45\), without using Mathematical tables.
(ii) Hence, solve \(x^{0.8265} = 45\).
(b) Use Mathematical tables to evaluate \(\sqrt{\frac{2.067}{0.0348 \times 0.538}}\)
A box contains identical balls of which 12 are red, 16 white and 8 blue. Three balls are drawn from the box one after the other without replacement. Find the probability that :
(a) three are red;
(b) the first is blue and the other two are red;
(c) two are white and one is blue.
(a) Simplify \(\frac{3}{m + 2n} – \frac{2}{m – 3n}\)
(b) A number is made up of two digits. The sum of the digits is 11. If the digits are interchanged, the original number is increased by 9. Find the number.
A simple measuring device is used at points X and Y on the same horizontal level to measure the angles of elevation of the peak P of a certain mountain. If X is known to 5,200m above sea level, /XY/ = 4,000m and the measurements of the angles of elevation of P at X and Y are 15° and 35° respectively, find the height of the mountain. (Take \(\tan 15 = 0.3\) and \(\tan 35 = 0.7\))
The universal set \(\varepsilon\) is the set of all integers and the subset P, Q, R of \(\varepsilon\) are given by:
\(P = {x : x < 0} ; Q = {… , -5, -3, -1, 1, 3, 5} ; R = {x : -2 \leq x < 7}\)
(a) Find \(Q \cap R\).
(b) Find \(R’\) where R’ is the complement of R with respect to \(\varepsilon\).
(c) Find \(P’ \cup R’\)
(d) List the members of \((P \cap Q)’\).
(a) Simplify, without using Mathematical tables: \(\log_{10} (\frac{30}{16}) – 2 \log_{10} (\frac{5}{9}) + \log_{10} (\frac{400}{243})\)
(b) Without using Mathematical tables, calculate \(\sqrt{\frac{P}{Q}}\) where \(P = 3.6 \times 10^{-3}\) and \(Q = 2.25 \times 10^{6}\), leaving your answer in standard form.
| Number | 1 | 2 | 3 | 4 | 5 | 6 |
| No of times | 25 | 30 | 45 | 28 | 40 | 32 |
A die rolled 200 times. The outcome obtained are shown in the table above.
What is the probability of obtaining a number less than 3 ?
- A. 0.125
- B. 0.150
- C. 0.275
- D. 0.500
- E. 0.725
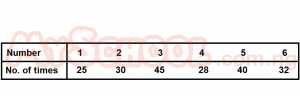
A die is rolled 200 times the outcomes obtained are shown in the table below.
Find the probability of obtaining 2.
- A. 0.002
- B. 0.015
- C. 0.15
- D. 16
- E. 0.2
What is the probability that the total sum of seven would appear in toss of a fair die?
- A. 5/36
- B. 1/6
- C. 7/36
- D. 5/6
- E. 1
What is the probability of having an even number in a single toss of a fair die?
- A. 1/6
- B. 1/3
- C. 1/2
- D. 2/3
- E. 5/6
A fair die is rolled once. What is the probability of obtaining a number less than 3?
- A. 1/6
- B. 1/3
- C. 2/3
- D. 1/2
- E. 5/6
What is the probability that an integer selected from the set of integers (20, 21, …., 30) is a prime number?
- A. 2/11
- B. 5/11
- C. 6/11
- D. 9/11
- E. 2/3
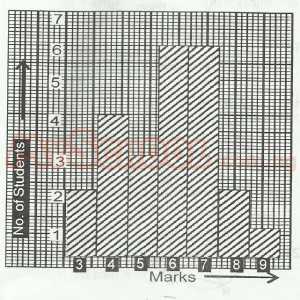
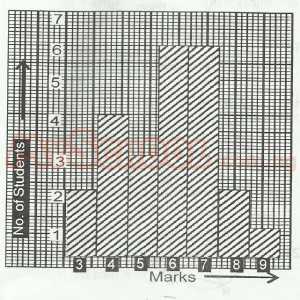
How many students scored less than 7 marks?
- A. 9
- B. 15
- C. 18
- D. 21
- E. 25
The distribution by state of 840 students in the Faculty of Science of a Nigerian University in a certain session is as follows:
| Bendel | 45 |
| kwara | 410 |
| Ogun | 105 |
| Ondo | 126 |
| Oyo | 154 |
In a pie chart drawn to represent this distribution, the angle subtended by Ondo is
- A. 36o
- B. 42o
- C. 45o
- D. 48o
- E. 54o