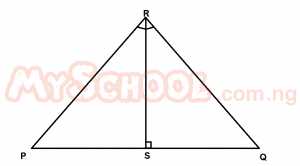
In the diagram above, |QR| = 12cm and |QS| = 10cm. If ∠PQR = 90°, ∠RSQ = 90° and PSQ is a straight line, find |PS|
- 3.3cm
-
4.4cm
- 5cm
- 5.5cm
- 6.6cm
The correct answer is: B
Explanation
\(\frac{PQ}{RQ} = \frac{RQ}{SQ}\) (Similar triangles)
\(\therefore \frac{PS + 10}{12} = \frac{12}{10}\)
\(10 (PS + 10) = 12 \times 12\)
\(10 PS + 100 = 144 \implies 10 PS = 44\)
\(PS = 4.4 cm\)