A simple measuring device is used at points X and Y on the same horizontal level to measure the angles of elevation of the peak P of a certain mountain. If X is known to 5,200m above sea level, /XY/ = 4,000m and the measurements of the angles of elevation of P at X and Y are 15° and 35° respectively, find the height of the mountain. (Take \(\tan 15 = 0.3\) and \(\tan 35 = 0.7\))
Explanation
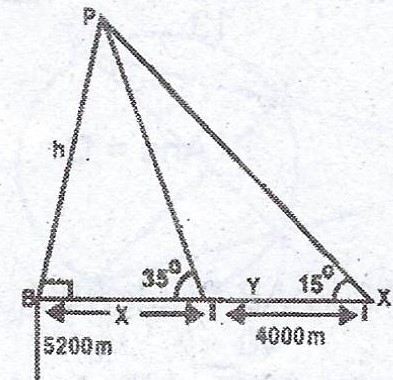
In \(\Delta\) BPY, \(\tan 35° = \frac{h}{x}\)
\(h = x \tan 35 = 0.7 x ... (1)\)
In \(\Delta\) BPX, \(\frac{h}{x + 4000} = \tan 15\)
\(\frac{h}{x + 4000} = 0.3\)
\(h = 0.3 (x + 4000) = 0.3x + 1200 ... (2)\)
Equating (1) and (2) as the values of h, we have
\(0.7x = 0.3x + 1200 \implies 0.7x - 0.3x = 1200\)
\(0.4x = 1200 \times x = \frac{1200}{0.4} = 3000m\)
\(\therefore h = 0.7x = 0.7 (3000) = 2100m\)
\(\text{The total height = } 5200m + 2100m = 7300m\)

