(a) Copy and complete the following table of values for \(y = 3\sin 2\theta – \cos \theta\).
| \(\theta\) | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| y | -1.0 | 0 | 1.0 |
(b) Using a scale of 2cm to 30° on the \(\theta\) axis and 2cm to 1 unit on the y- axis, draw the graph of \(y = 3 \sin 2\theta – \cos \theta\) for \(0° \leq \theta \leq 180°\).
(c) Use your graph to find the : (i) solution of the equation \(3 \sin 2\theta – \cos \theta = 0\), correct to the nearest degree; (ii) maximum value of y, correct to one decimal place.
Explanation
(a)
| \(\theta\) | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| y | -1.0 | 1.732 | 2.098 | 0 | -2.098 | -1.732 | 1.0 |
(b) 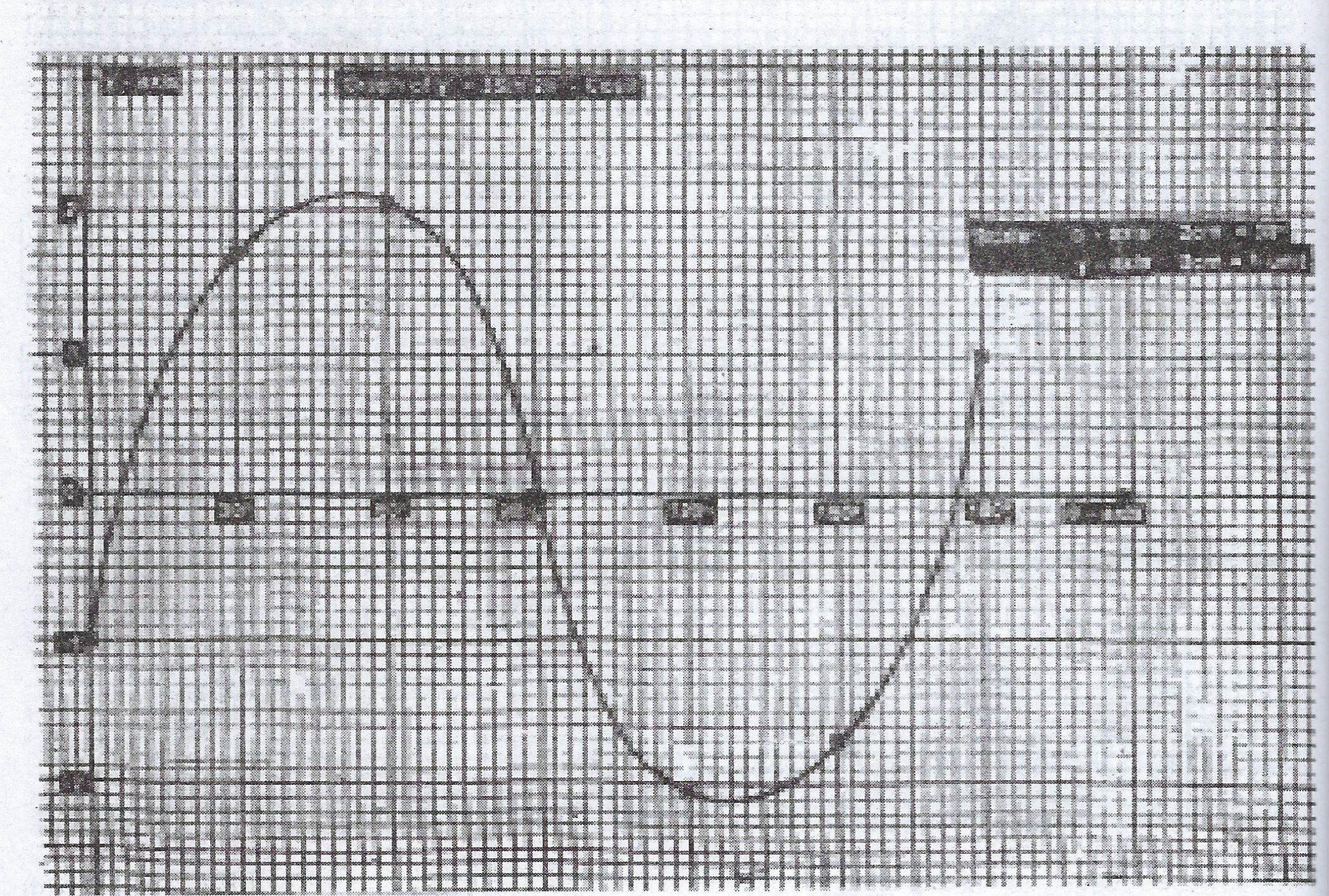
(c)(i) Solution of \(3 \sin 2 \theta - \cos \theta = 0\) is at y = 0
= \(9.30°, 80°, 174°\)
(ii) Maximum value of y = 2.098 \(\approxeq\) 2.1 (to 1 decimal place)

