P and Q are two points on latitude 55°N and their longitudes are 33°W and 20°E respectively. Calculate the distance between P and Q measured along
(a) the parallel of latitude ;
(b) a great circle.
[Take \(\pi = \frac{22}{7}\) and radius of the earth = 6400km].
Explanation
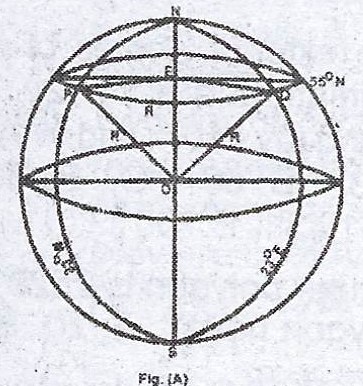
(a) Angular difference = 33° + 23° = 56°
Distance PQ along parallel of latitude = \(\frac{56}{360} \times 2 \pi r\)
where r = R cos 55°
\(\therefore |PQ| = \frac{56}{360} \times 2 \times \frac{22}{7} \times 6400 \cos 55\)
= \(3589.46 km \approxeq 3589 km\) (to the nearest degree)
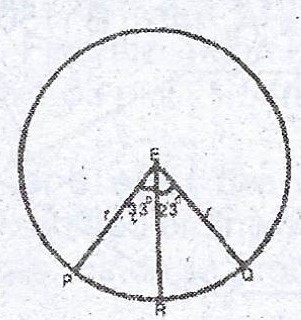
(b) \(|PO|^{2} = r^{2} + r^{2} - 2r^{2} \cos 56° = R^{2} + R^{2} - 2R^{2} \cos \theta \)
= \(2r^{2} - 2r^{2} \cos 56° = 2R^{2} - 2R^{2} \cos \theta\)
But \(r = R cos 55° = 6400 \times 0.5736 = 3671\)
\(\therefore 2r^{2} (1 - \cos 56°) = 2R^{2} (1 - \cos \theta)\)
\(2 \times 3671^{2} ( 1 - 0.5592) = 2 \times 6400^{2} (1 - \cos \theta)\)
\(1 - \cos \theta = \frac{2 \times 3671^{2} \times 0.4408}{2 \times 6400^{2}}\)
\(1 - \cos \theta = 0.1259\)
\(\cos \theta = 1 - 0.1259 = 0.8741\)
\(\theta = \cos^{-1} (0.8741) = 29.06°\)
\(\therefore\) Distance PQ along great circle = \(\frac{29.06}{360} \times 2 \times \frac{22}{7} \times 6400\)
= \(3247.34 km \approxeq 3247km\)

