(a) Two points X(32°N, 47°W) and Y(32°N, 25°E) are on the earth’s surface. If it takes an aeroplane 11 hours to fly from X to Y along the parallel of latitude, calculate its speed, correct to the nearest kilometre per hour. [Radius of the earth = 6400km; \(\pi = \frac{22}{7}\)]
(b) Two observers P and Q, 15metres apart observe a kite (K) in the same vertical plane and from the same side of the kite. The angles of elevation of the kite from P and Q are 35° and 45° respectively. Find the height of the kite to the nearest metre.
(a) The fourth term of an A.P is 37 and 6th term is 12 more than the fourth term . Find the first and seventh terms.
(b) If \(P = {1, 2, 3, 4}\) and \(Q = {3, 5, 6}\), find (i) \(P \cap Q\) ; (ii) \(P \cup Q\) ; (iii) \((P \cap Q) \cup Q\) ; (iv) \((P \cap Q) \cup P\).
(a) Copy and complete the following table of values for \(y = 2x^{2} – 9x – 1\).
| x | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | -1 | -8 | -11 | 17 |
(b) Using a scale of 2cm to represent 1 unit on the x- axis and 2cm to represent 5 units on the y- axis, draw the graph of \(y = 2x^{2} – 9x – 1\).
(c) Use your graph to find the : (i) roots of the equation \(2x^{2} – 9x = 4\), correct to one decimal place ; (ii) gradient of the curve \(y = 2x^{2} – 9x – 1\) at x = 3.
The table below gives the ages, to the nearest 5 years of 50 people.
| Age in years | 10 | 15 | 20 | 25 | 30 |
| No of people | 8 | 19 | 10 | 7 | 6 |
(a) Construct a cumulative frequency table for the distribution.
(b) Draw a cumulative frequency curve (Ogive)
(c) From your Ogive, find the : (i) median age ; (ii) number of people who are at most 15 years of age ; (iii) number of people who are between 20 and 25 years of age.
(a) Using a ruler and a pair of compasses only, construct (i) a triangle XYZ in which /YZ/ = 8cm, < XYZ = 60° and < XZY = 75°. Measure /XY/; (ii) the locus \(l_{1}\) of points equidistant from Y and Z ; (iii) the locus \(l_{2}\) of points equidistant from XY and YZ.
(b) Measure QY where Q is the point of intersection of \(l_{1}\) and \(l_{2}\).
A bag contains 12 white balls and 8 black balls, another contains 10 white balls and 15 black balls. If two balls are drawn, without replacement from each bag, find the probability that :
(a) all four balls are black ;
(b) exactly one of the four balls is white.
(a) If \(\log_{10} (3x – 1) – \log_{10} 2 = 3\), find the value of x.
(b) Use logarithm tables to evaluate \(\sqrt{\frac{0.897 \times 3.536}{0.00249}}\), correct to 3 significant figures.
The table below gives the frequency distribution of the marks obtained by some students in a scholarship examination.
| Scores (x) | 15 | 25 | 35 | 45 | 55 | 65 | 75 |
| Freq (f) | 1 | 4 | 12 | 24 | 18 | 8 | 3 |
(a) Calculate, correct to 3 significant figures, the mean mark.
(b) Find the : (i) mode ; (ii) range of the distribution.
(a) Divide \(11111111_{two}\) by \(101_{two}\)
(b) A sector of radius 6 cm has an angle of 105° at the centre. Calculate its:
(i) perimeter ; (ii) area . [Take \(\pi = \frac{22}{7}\)]
(a) A tower and a building stand on the same horizontal level. From the point P at the bottom of the building, the angle of elevation of the top, T of the tower is 65°. From the top Q of the building, the angle of elevation of the point T is 25°. If the building is 20m high, calculate the distance PT.
(b) Hence or otherwise, calculate the height of the tower. [Give your answers correct to 3 significant figures].
(a) Evaluate, without using mathematical tables, \(17.57^{2} – 12.43^{2}\).
(b) Prove that angles in the same segment of a circle are equal.
(a) Given that \(3 \times 9^{1 + x} = 27^{-x}\), find x.
(b) Evaluate \(\log_{10} \sqrt{35} + \log_{10} \sqrt{2} – \log_{10} \sqrt{7}\)
The length of an exercise book is given as 20cm correct to the nearest centimeter. In which of the following ranges of possible measurement does the actual length lie?
- A. 19.5 - 20.4cm
- B. 19.1 - 20.9cm
- C. 19.9 - 20.1cm
- D. 19.95 - 20.05cm
- E. 19 - 21cm
Find the probability that a number selected from the number 30 to 50 inclusive is a prime
- A. 1/4
- B. 5/21
- C. 2/7
- D. 3/10
- E. 1/3
Two cards are drawn one after the other with replacement from a well-shuffled ordinary deck of 52 cards containing four Aces. Find the probability that they are both Aces
- A. 1/221
- B. 1/169
- C. 1/52
- D. 1/26
- E. 1/13
The mean heights of the three groups of students consisting of 20, 16 and 14 students are 1.67m, 1.50m and 1.40m respectively. Find the mean height of the students
- A. 1.52m
- B. 1.53m
- C. 1.54m
- D. 1.55m
- E. 1.56m
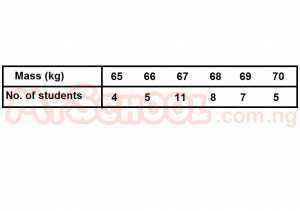
The percentage of the students with mass less than 69kg is
- A. 56%
- B. 62.5%
- C. 68%
- D. 70%
- E. 87.5%
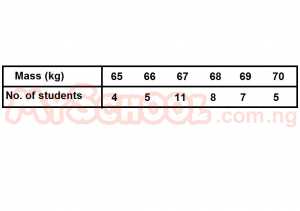
The median of the distribution is
- A. 9.5kg
- B. 11kg
- C. 67kg
- D. 65.5kg
- E. 68kg
cos 57o has the same value as
- A. sin 213o
- B. -cos 303o
- C. sin 147o
- D. cos 123o
- E. cos237o
The bearing of Q from P is 122o, what is the bearing of P from Q?
- A. 212o
- B. 238o
- C. 248o
- D. 292o
- E. 302o
A ladder 6m long leans against a vertical wall so that it makes an angle of 60o with the wall. Calculate the distance of the foot of the ladder from the wall
- A. 3m
- B. 6m
- C. 2√3m
- D. 3√3m
- E. 6√3m


