(a) A tower and a building stand on the same horizontal level. From the point P at the bottom of the building, the angle of elevation of the top, T of the tower is 65°. From the top Q of the building, the angle of elevation of the point T is 25°. If the building is 20m high, calculate the distance PT.
(b) Hence or otherwise, calculate the height of the tower. [Give your answers correct to 3 significant figures].
Explanation
(a) 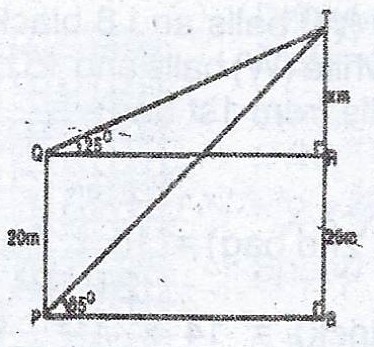
\(< QPB = 90° - 65° = 25°\)
Also, \(< TQP = 90° + 25° = 115°\)
\(\therefore < QTP = 180° - (25° + 115°) = 40°\)
Using sine rule, \(\frac{PQ}{\sin 40°} = \frac{PT}{\sin 115°}\)
\(PT = \frac{20 \sin 115°}{\sin 40°} = \frac{20 \sin 65°}{\sin 40°}\)
= \(28.199m \approxeq 28.2m\) (to 3 sig. fig)
(b) Height of the tower = ST
\(\sin 65 = \frac{ST}{PT} = \frac{ST}{28.199}\)
\(ST = 28.199 \times \sin 65° = 25.557m\)
\(\approxeq 25.6m\) (to 3 sig. figs)

