(a) Two points X(32°N, 47°W) and Y(32°N, 25°E) are on the earth’s surface. If it takes an aeroplane 11 hours to fly from X to Y along the parallel of latitude, calculate its speed, correct to the nearest kilometre per hour. [Radius of the earth = 6400km; \(\pi = \frac{22}{7}\)]
(b) Two observers P and Q, 15metres apart observe a kite (K) in the same vertical plane and from the same side of the kite. The angles of elevation of the kite from P and Q are 35° and 45° respectively. Find the height of the kite to the nearest metre.
Explanation
(a) 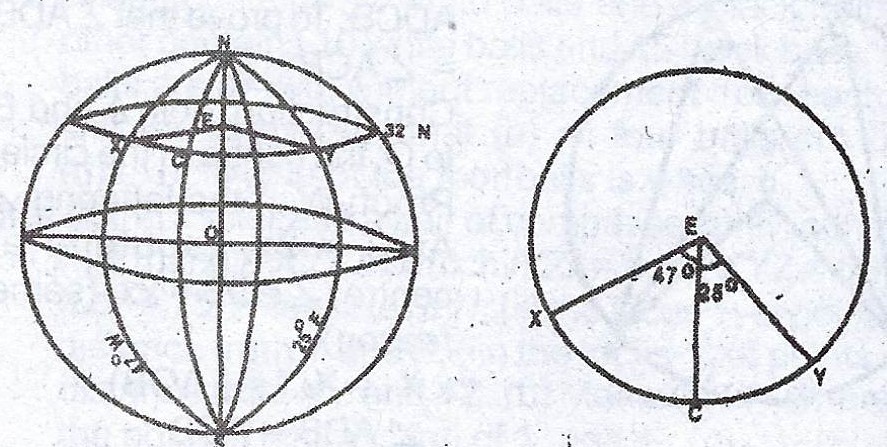
Difference in longitude = 47° + 25° = 72°
Distance /XY/ = \(\frac{\theta}{360°} \times 2\pi r\)
Where \(r = R \cos 32°\)
\(\therefore /XY/ = \frac{72}{360} \times 2 \times \frac{22}{7} \times 6400 \times \cos 32\)
= \(2 \times \frac{22}{7} \times 1280 \times 0.8480\)
= \(6822.765km\)
\(Speed = \frac{Distance}{Time}\)
= \(\frac{6822.766}{11} = 620.25 km/h\)
(b) 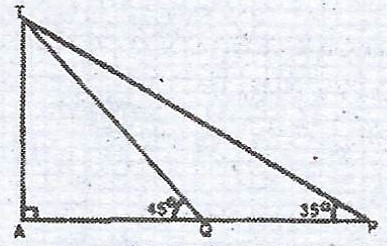 \
\
\( <TQP = 180° - 45° = 135°\) (angles on a straight line)
\(< QTP = 180° - (135° + 35°) = 10°\) (sum of angles in a triangle)
\(\frac{TQ}{\sin 35°} = \frac{15}{\sin 10°}\)
\(\therefore TQ = \frac{15 \sin 35°}{\sin 10°}\)
= \(49.546m\)
\(\therefore \sin 45° = \frac{TA}{TQ}\)
\(\sin 45° = \frac{TA}{49.546}\)
\(TA = 49.546 \times 0.7071 = 35.03m\)
\(\therefore\) The height of the kite = 35m (correct to the nearest whole number)

