A box contains 5 blue balls, 3 black balls and 2 red balls of the same size. A ball is selected at random from the box and then replaced. A second ball is then selected. Find the probability of obtaining
(a) two red balls ;
(b) two blue balls or two black balls ;
(c) one black and one red ball in any order.
The table shows the scores of 2000 candidates in an entrance examination into a private secondary school.
| % Mark | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 |
|
No of pupils |
68 | 184 | 294 | 402 | 480 | 310 | 164 | 98 |
(a) Prepare a cumulative frequency table and draw the cumulative frequency curve for the distribution.
(b) Use your curve to estimate the : (i) cut off mark, if 300 candidates are to be offered admission ; (ii) probability that a candidate picked at random, scored at least 45%.
(a) A man travels from a village X on a bearing of 060° to a village Y which is 20km away. From Y, he travels to a village Z, on a bearing of 195°. If Z is directly east of X, calculate, correct to three significant figures, the distance of :
(i) Y from Z ; (ii) Z from X .
(b) An aircraft flies due South from an airfield on latitude 36°N, longitude 138°E to an airfield on latitude 36°S, longitude 138°E.
(i) Calculate the distance travelled, correct to three significant figures ; (ii) if the speed of the aircraft is 800km per hour, calculate the time taken, correct to the nearest hour.
[Take \(\pi = \frac{22}{7}\), R = 6400km].
(a) Using a ruler and a pair of compasses only, construct triangle ABC with /AB/ = 7.5cm, /BC/ = 8.1cm and < ABC = 105°.
(b) Locate a point D on BC such that /BD/ : /DC/ is 3 : 2.
(c) Through D, construct a line I perpendicular to BC.
(d) If the line I meets AC at P, measure /BP/.
(a) Copy and complete the table for the relation \(y = 2 \cos 2x – 1\).
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| \(y = 2\cos 2x – 1\) | 1.0 | 0 | 1.0 |
(b) Using a scale of 2cm = 30° on the x- axis and 2cm = 1 unit on the y- axis, draw the graph of \(y = 2 \cos 2x – 1\) for \(0° \leq x \leq 180°\).
(c) On the same axis, draw the graph of \(y = \frac{1}{180} (x – 360)\)
(d) Use your graphs to find the : (i) values of x for which \(2 \cos 2x + \frac{1}{2} = 0\); (ii) roots of the equation \(2 \cos 2x – \frac{x}{180} + 1 = 0\).
(a) Given that \(p = x + ym^{3}\), find m in terms of p, x and y.
(b) Using the method of completing the square, find the roots of the equation \(x^{2} – 6x + 7 = 0\), correct to 1 decimal place.
(c) The product of two consecutive positive odd numbers is 195. By constructing a quadratic equation and solving it, find the two numbers.
(a) Using mathematical tables, find ; (i) \(2 \sin 63.35°\) ; (ii) \(\log \cos 44.74°\);
(b) Find the value of K given that \(\log K – \log (K – 2) = \log 5\);
(c) Use logarithm tables to evaluate \(\frac{(3.68)^{2} \times 6.705}{\sqrt{0.3581}}\)
The frequency table shows the marks scored by 32 students in a test.
| Marks scored | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| No of students | 2 | 3 | 4 | 4 | 4 | 4 | 5 | 3 | 2 | 1 |
Find the :
(a)(i) mean ; (ii) median ; (iii) mode of the marks;
(b) percentage of the students who scored at least 8 marks.
(a) A pack of 52 playing cards is shuffled and a card is drawn at random. Calculate the probability that it is either a five or a red nine.
[Hint : There are 4 fives and 2 red nines in a pack of 52 cards]
(b) P, Q and R are points in the same horizontal plane. The bearing of Q from P is 150° and the bearing of R from Q is 060°. If /PQ/ = 5m and /QR/ = 3m, find the bearing of R from P, correct to the nearest degree.
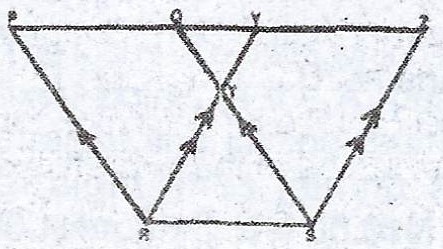
(a) In the diagram, PQSR and SRYZ are parallelograms and PQYZ is a straight line. If /QY/ = 2cm and /RS/ = 3cm, find /PZ/.
(b) P and Q are two towns on the earth’s surface on latitude 56°N. Thei longitudes are 25°E and 95°E respectively. Find the distance PQ along their parallel of latitude, correct to the nearest km. [Take radius of the earth as 6400km and \(\pi = \frac{22}{7}\)]
The quantity y is partly constant and partly varies inversely as the square of x.
(a) Write down the relationship between x and y.
(b) When x = 1, y = 11 and when x = 2, y = 5, find the value of y when x = 4.
(a) Factorise : \(px – 2px – 4qy + 2py\)
(b) Given that the universal set U = {1, 2, 3, 4,5, 6, 7, 8, 9, 10}, P = {1, 2, 4, 6, 10} and Q = {2, 3, 6, 9}; show that \((P \cup Q)’ = P’ \cap Q’\)
From a box containing 2 red, 6 white and 5 black balls, a ball is randomly selected. What is the probability that the selected ball is black?
- A. 2/13
- B. 5/13
- C. 5/11
- D. 5/6
- E. 11/13
Two fair dice are tossed together once. Find the probability that the sum of the outcome is at least 10.
- A. 1/12
- B. 5/ 36
- C. 1/ 6
- D. 1/4
- E. 5/18
Find the median of the following numbers 2.64, 2.50, 2.72, 2.91 and 2.35.
- A. 2.91
- B. 2.72
- C. 2.64
- D. 2.50
- E. 2.35
The mean of 20 observations in an experiment is 4, lf the observed largest value is 23, find the mean of the remaining observations.
- A. 4
- B. 3
- C. 2.85
- D. 2.60
- E. 2.56
What is the mode of the numbers 8, 10, 9, 9, 10, 8, 11, 8, 10, 9, 8 and 14?
- A. 8
- B. 9
- C. 10
- D. 11
- E. 14
The bearing of two points Q and R from a point P are 030° and 120° respectively, lf /PQ/ = 12 m and /PR/ = 5 m, find the distance QR.
- A. 13m
- B. 11m
- C. 9m
- D. 7m
- E. 5m

In the diagram above, ∠PRQ = 90°, ∠QPR = 30° and /PQ/ = 10 cm. Find y.
- A. 6cm
- B. 5cm
- C. 4cm
- D. 3cm
- E. 2cm
Without using tables, find the value of \(\frac{\sin 20°}{\cos 70°} + \frac{\cos 25°}{\sin 65°}\)
- A. 2
- B. 1
- C. o
- D. -1
- E. -2

In ΔABC above, BC is produced to D, /AB/ = /AC/ and ∠BAC = 50o. Find ∠ACD
- A. 50o
- B. 60o
- C. 65o
- D. 100o
- E. 115o


