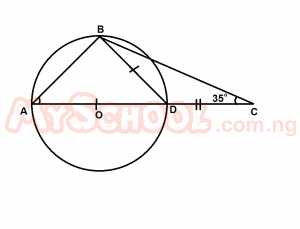
In the diagram above; O is the centre of the circle and |BD| = |DC|. If ∠DCB = 35°, find ∠BAO.
-
20o
- 25o
- 30o
- 35o
- 40o
The correct answer is: A
Explanation
< DBC = 35° (base angles of an isosceles triangle)
< CDB = 180° - (35° + 35°)
= 110°
< ADB = 70°; < ABD = 90°(< in a semi-circle)
\(\therefore\) < BAO = 180° - (70° + 90°)( sum of <s in a triangle)
= 20°