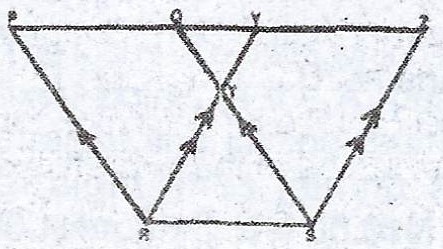
(a) In the diagram, PQSR and SRYZ are parallelograms and PQYZ is a straight line. If /QY/ = 2cm and /RS/ = 3cm, find /PZ/.
(b) P and Q are two towns on the earth’s surface on latitude 56°N. Thei longitudes are 25°E and 95°E respectively. Find the distance PQ along their parallel of latitude, correct to the nearest km. [Take radius of the earth as 6400km and \(\pi = \frac{22}{7}\)]
Explanation
(a) \(/QY/ = 2cm; /RS/ = 3cm\)
\(\therefore /YZ/ = /RS/ = /PQ/ = 3cm\) (opp sides of a parallelogram)
But \(/PZ/ = /PQ/ + /QY/ + /YZ/\)
\(\therefore /PZ/ = 3cm + 2cm + 3cm = 8cm\)
(b) Difference in longitude = 95° - 25° = 70°
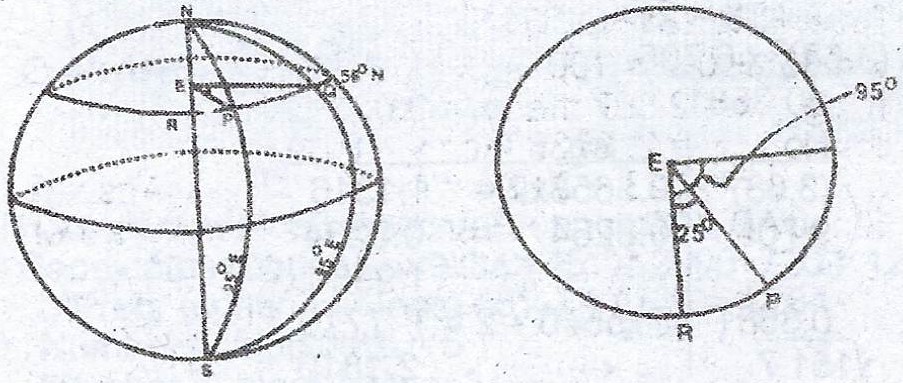
Distance PQ = \(\frac{70}{360} \times 2\pi R \cos \theta\)
= \(\frac{70}{360} \times 2 \times \frac{22}{7} \times 6400 \cos 56\)
= \(\frac{7}{36} \times 2 \times \frac{22}{7} \times 6400 \times 0.5592\)
= \(4374.19 km \approxeq 4374 km\) (to the nearest km)

