(a) A pack of 52 playing cards is shuffled and a card is drawn at random. Calculate the probability that it is either a five or a red nine.
[Hint : There are 4 fives and 2 red nines in a pack of 52 cards]
(b) P, Q and R are points in the same horizontal plane. The bearing of Q from P is 150° and the bearing of R from Q is 060°. If /PQ/ = 5m and /QR/ = 3m, find the bearing of R from P, correct to the nearest degree.
Explanation
(a) Total no of cards = 52; No of fives = 4; No of red nines = 2.
Prob(of 5) = \(\frac{4}{52} = \frac{1}{13}\)
Prob(red nine) = \(\frac{2}{52} = \frac{1}{26}\)
\(\therefore\) Prob (of 5 or red nine) = \(\frac{1}{13} + \frac{1}{26} = \frac{3}{26}\)
(b) \(\tan < RPQ = \frac{3}{5} = 0.6\)
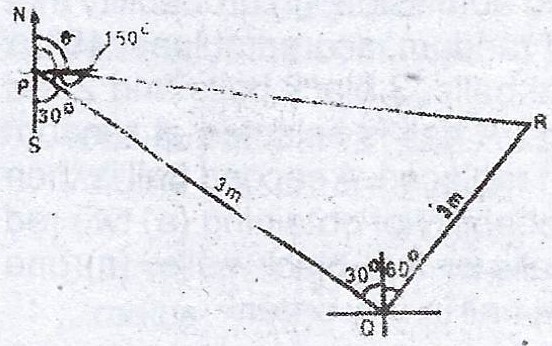
\(< RPQ = 30.96°\)
\(\therefore\) Bearing of R from P = 150° - 30.96° = 119.04°
\(\approxeq\) 119° (to the nearest degree).

