(a) Copy and complete the table for the relation \(y = 2 \cos 2x – 1\).
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| \(y = 2\cos 2x – 1\) | 1.0 | 0 | 1.0 |
(b) Using a scale of 2cm = 30° on the x- axis and 2cm = 1 unit on the y- axis, draw the graph of \(y = 2 \cos 2x – 1\) for \(0° \leq x \leq 180°\).
(c) On the same axis, draw the graph of \(y = \frac{1}{180} (x – 360)\)
(d) Use your graphs to find the : (i) values of x for which \(2 \cos 2x + \frac{1}{2} = 0\); (ii) roots of the equation \(2 \cos 2x – \frac{x}{180} + 1 = 0\).
Explanation
(a)
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| \(y = 2\cos 2x - 1\) | 1.0 | 0 | -2 | -3 | -2 | 0 | 1.0 |
(b) 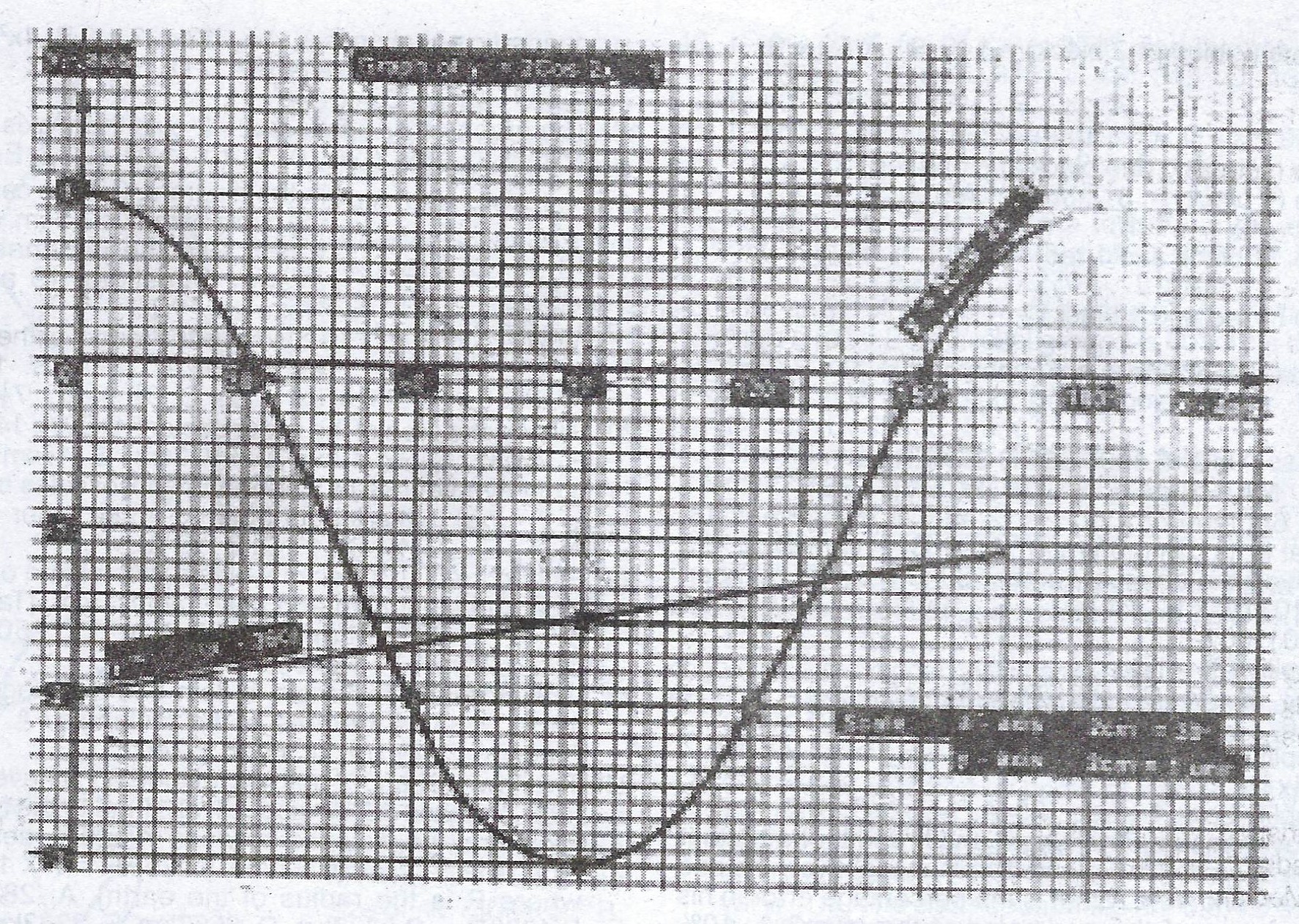
(c)
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| \(y = \frac{1}{180} (x - 360)\) | -2.0 | -1.83 | -1.67 | -1.5 | -1.33 | -1.17 | -1.0 |
(d)(i) \(2 \cos 2x + \frac{1}{2} = 0\)
\(2 \cos 2x + \frac{1}{2} - 1\frac{1}{2} = -1\frac{1}{2}\)
\(2 \cos 2x - 1 = -1\frac{1}{2}\)
The values of x at \(2 \cos 2x + \frac{1}{2} = 0\) are x = 51° and 129°.
(ii) \(2 \cos 2x - \frac{x}{180} + 1 = 0\)
\(2 \cos 2x - 1 = \frac{1}{180} (x - 360)\)
The values of x is where the two graphs intersect; which are at x = 54° and 132°.

