(a) A man travels from a village X on a bearing of 060° to a village Y which is 20km away. From Y, he travels to a village Z, on a bearing of 195°. If Z is directly east of X, calculate, correct to three significant figures, the distance of :
(i) Y from Z ; (ii) Z from X .
(b) An aircraft flies due South from an airfield on latitude 36°N, longitude 138°E to an airfield on latitude 36°S, longitude 138°E.
(i) Calculate the distance travelled, correct to three significant figures ; (ii) if the speed of the aircraft is 800km per hour, calculate the time taken, correct to the nearest hour.
[Take \(\pi = \frac{22}{7}\), R = 6400km].
Explanation
(a) < XZY = 180° - (30° + 45°) = 105°
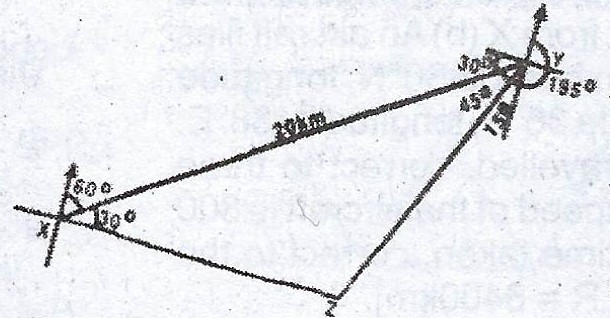
\(\frac{20}{\sin 105°} = \frac{YZ}{\sin 30°}\)
\(YZ = \frac{20 \sin 30°}{\sin 105°} = 10.35km\)
\(\approxeq 10.4km \) (to 3 sig. figs)
(ii) \(\frac{20}{\sin 75} = \frac{XZ}{\sin 45}\)
\(XZ = \frac{20 \sin 45}{\sin 75} = 14.64km\)
\(\approxeq 14.6km\) ( to 3 sig. figs)
(b) Let P and Q be two airfields.
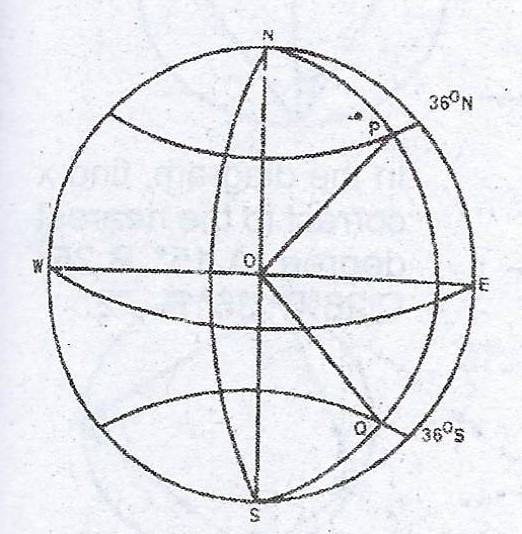
Difference in latitude = 36° + 36° = 72°
(i) Distance between P and Q = \(\frac{72}{360} \times 2 \times \frac{22}{7} \times 6400\)
= \(\frac{22}{7} \times 2560\)
= \(8,045.71km \approxeq 8,050 km\) (3 sig. figs)
(ii) Time taken = \(\frac{8,045.71}{800} = 10.06 hours\)
\(\approxeq 10hours\) (to the nearest hour)

