Two men P and Q set off from a base camp R, prospecting for oil. P moves 20km on a bearing of 205° and Q moves 15km on a bearing of 060°. Calculate the:
(a) distance of Q from P ;
(b) bearing of Q from P.
(Give your answer in each case to the nearest whole number)
(a) P and Q are points on the parallel of latitude 68.7°S, their longitudes being 124°W and 56°E respectively. What is their distance apart measured along the parallel of latitude? [Take R = 6400km, \(\pi = 3.142\)]. (Give your answers to 3 significant figures).
(b) A bag contains four red, three white and five green balls. (i) If one ball is picked at random, what is the probability that it is not green? (ii) if two balls are picked at random without replacement, what is the probability that one is red and the other white?
(a) Make d the subject of the formula \(S = \frac{n}{2}[2a + (n – 1) d]\).
(b) (i) 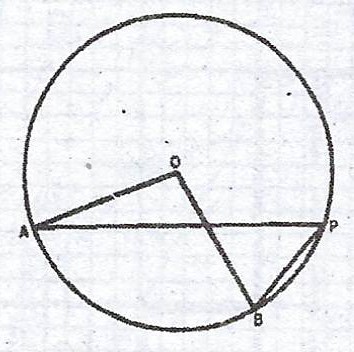
In the diagram, O is the centre of the circle, A, B and P are points on the circumference. Prove that < AOB = 2 < APB.
(ii) 
Find the angles x, v and z in the diagram.
(a) Copy and complete the table for \(y = 3x^{2} – 5x – 7\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| \(y = 3x^{2} – 5x – 7\) | 35 | -7 | -9 | 5 |
(b) Using a scale of 2cm = 1 unit along the x- axis and 2cm = 5 units along the y- axis, draw the graph of \(y = 3x^{2} – 5x – 7\).
(c) On the same axis, draw the graph of \(y + 3x + 2 = 0\).
(d) From your graph, find the : (i) range of values of x for which \(3x^{2} – 5x – 7 < 0\) ; (ii) roots of the equation \(3x^{2} – 2x – 5 = 0\).
(a) Find the number N such that when \(\frac{1}{3}\) of it is added to 8, the result is the same as when \(\frac{1}{2}\) of it is subtracted from 18.
(b) Using a ruler and a pair of compasses only, construct a trapezium ABCD, in which the parallel sides AB and DC are 4 cm apart. < DAB = 60°, /AB/ = 8 cm and /BC/ = 5 cm. Measure /DC/.
(a) The universal set U is the set of integers, P, Q and R are subsets of U defined as follows:
\(P = x : x \leq 2 \) ; \(Q = x : -7 < x < 15\) ; \(R = x : -2 \leq x < 19\).
Find (i) \(P \cap Q\) ; (ii) \(P \cap (Q \cup R’)\), where R’ is the complement of R with respect to U.
(b) The following data shows the marks of 40 students in a History examination.
41 52 37 56 63 48 65 46 54 32 51 66 74 23 35 61 58 44 49 53 45 57 56 38 59 28 50 49 67 56 36 45 79 68 43 56 26 47 55 71.
(i) Form a grouped frequency table with the class intervals 20 – 29, 30 – 39, 40 – 49 etc; (ii) Find the mean of the distribution.
(a) Without using tables, find the value of \(\frac{0.45 \times 0.91}{0.0117}\)
(b) Find the number which is exactly halfway between \(1\frac{6}{7}\) and \(2\frac{11}{28}\).
(c) If each interior angle of a regular polygon is five times the exterior angle, how many sides has the polygon?
(d) Calculate the volume of the material used in making a pipe 20cm long, with an internal diameter 6cm and external diameter 8cm. [Take \(pi = \frac{22}{7}\)].
(a) ABCD is a trapezium with AB parallel to DC and /AD/ = /AB/. If < BAD = 106°, find < BDC.
(b) The table below shows the distribution of 20 cards labelled A – E.
| Card | A | B | C | D | E |
| Frequency | 3 | 4 | 7 | 5 | 1 |
(i) If a card is selected at random from the pack, what is the probability that the card is E? (ii) If two cards are selected at random one after the other without replacement from the pack, what is the probability that one of the two cards is B?
(a) If \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), calculate without using tables, the value of \(\log_{10} 0.72\).
(b) A hawk on top of a tree, 20 metres high views a chick on the ground at an angle of depression of 39°. Find, correct to 2 significant figures, the distance of the chick from the bottom of the tree.
The table below shows the marks obtained by forty pupils in a Mathematics test.
| Marks | 0 – 9 | 10 – 19 | 20 – 29 | 30 – 39 | 40 – 49 | 50 – 59 |
| No of pupils | 4 | 5 | 6 | 12 | 8 | 5 |
(a) Draw a histogram for the mark distribution ;
(b) Use your histogram to estimate the mode ;
(c) Calculate the median of the distribution.
(a) Solve the simultaneous equation : \(6y + 5x = 12 ; 4y – 3x = 11\).
(b) 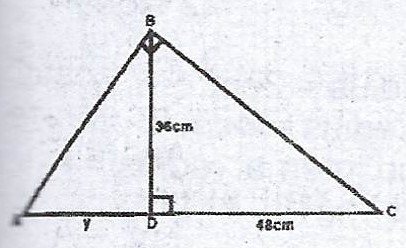
In the diagram, ADC is a straight line. /CD/ = 48 cm, /BD/ = 36 cm and /AD/ = y cm. Find the value of y.
A shopkeeper buys 40 kg of fruits for N120.00. He sells 20 kg at N5.00 per kg, 10 kg at N3.00 per kg, 5 kg at N2.00 per kg and the remaining 5 kg at 50k per kg. Calculate the :
(a) amount he realises from the sales ;
(b) total profit / loss ;
(c) percentage profit/ loss on his outlay of N120.00.

The table gives the distribution of outcomes obtained when a die was rolled 100 times.
What is the experimental probability that it shows at most 4 when rolled again?
- A. 8/25
- B. 12/25
- C. 13/25
- D. 2/3
- E. 17/25
A bag contains 3 red, 4 black and 5 green identical balls. Two balls are picked at random, one after the other without replacement. Find the probability that one is red and the other is green
- A. 2/3
- B. 5/11
- C. 5/22
- D. 5/24
- E. 5/48
What percentage of observation lie outside interquartile range of any distribution?
- A. 121/2%
- B. 25%
- C. 50%
- D. 621/2 %
- E. 75%
The marks obtained by pupils of class are grouped as shown below; 0 – 4, 5 – 9,10 -14, 15 -19. Which of the following is/are not true? l. The mid values of the grouped marks are 2, 7, 12 and 17. II The class interval is 4. III The class boundaries are 0.5, 4.5, 9.5, 14.5 and 19.5
- A. I only
- B. II only
- C. III only
- D. I and II only
- E. II and III only
The cumulative frequency curve may be used to find the
- A. variance
- B. standard deviation
- C. mode
- D. median
- E. mean

The number of goals scored by a football team in 20 matches is shown in the table above
What is the modal goal scored?
- A. o
- B. 1
- C. 2
- D. 5
- E. 7

The number of goals scored by a football team in 20 matches is shown in the table above
What is the mean goal scored?
- A. 0.75
- B. 1.75
- C. 1.9
- D. 2
- E. 2.15
The angle of elevation of the top X of a vertical pole from a point P on a level ground is 60o. The distance from P to the foot of the pole is 55m. Without using tables, find the height of the pole.
- A. 50/3m
- B. 50m
- C. 55√3m
- D. 60m
- E. 65m
A town P is 150km from a town Q in the direction 050o. What is the bearing of Q from P?
- A. 050o
- B. 130o
- C. 230o
- D. 270o
- E. 310o


