(a) If \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), calculate without using tables, the value of \(\log_{10} 0.72\).
(b) A hawk on top of a tree, 20 metres high views a chick on the ground at an angle of depression of 39°. Find, correct to 2 significant figures, the distance of the chick from the bottom of the tree.
Explanation
(a) \(\log_{10} 0.72 =\log_{10} (\frac{72}{100})\)
= \(\log_{10} 72 - \log_{10} 100\)
= \(72 = 2^{3} \times 3^{2}\)
\(\log_{10} 72 = \log_{10} 2^{3} + \log_{10} 3^{2} = 3\log_{10} 2 + 2 \log_{10} 3\)
= \(3(0.3010) + 2(0.4771) = 0.9030 + 0.9542 = 1.8572\)
\(\therefore \log_{10} 0.72 \equiv \log_{10} 72 - \log_{10} 100\)
= \(1.8572 - 2 = -0.1428\)
(b)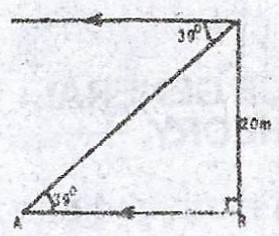 
\(\tan 39° = \frac{20}{AB} \)
= \(\frac{20}{\tan 39°}\)
\(AB = 24.698 m \approxeq 25m\)