Two men P and Q set off from a base camp R, prospecting for oil. P moves 20km on a bearing of 205° and Q moves 15km on a bearing of 060°. Calculate the:
(a) distance of Q from P ;
(b) bearing of Q from P.
(Give your answer in each case to the nearest whole number)
Explanation
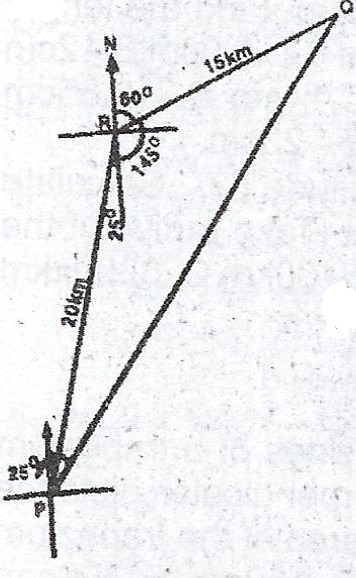
(a) By cosine rule, \(/PQ/^{2} = 20^{2} + 15^{2} - 2 \times 20 \times 15 \times \cos 145°\)
= \(400 + 225 - 600 \cos 145°\)
= \(625 + 600 \times 0.8192\)
= \(491.52 + 625\)
\(/PQ/^{2} = 1116.52 \implies /PQ/ = \sqrt{1116.52} = 33.41\)
\(\approxeq 33km\) ( to the nearest whole number)
(b) By sine rule,
\(\frac{\sin < QPR}{15} = \frac{\sin 145}{33.41}\)
\(\sin < QPR = \frac{15 \sin 145}{33.41}\)
\(\sin < QPR = \frac{15 \times 0.5736}{33.41} = 0.2575\)
\(< QPR = 14.92°\)
\(\therefore\) Bearing of Q from P = 25° + 14.92° = 39.92°.
\(\approxeq 40°\) (to nearest whole number)

