The table below shows the number of eggs laid by the chickens in a man’s farm in a year.
| No of eggs per year | No of chickens |
| 45 – 49 | 10 |
| 50 – 54 | 36 |
| 55 – 59 | 64 |
| 60 – 64 | 52 |
| 65 – 69 | 28 |
| 70 – 74 | 10 |
(a) Draw a cumulative frequency curve for the distribution.
(b) Use your graph to find the interquartile range.
(c) If a woman buys a chicken from the farm, what is the probability that the chicken lays at least 60 eggs in a year?
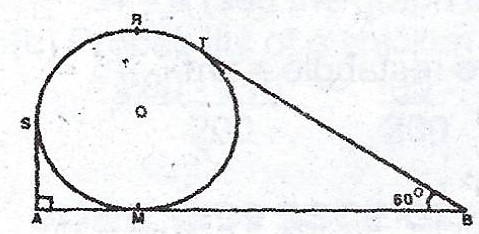
In the diagram, ASRTB represents a piece of string passing over a pulley of radius 10cm in a vertical plane. O is the centre of the pulley and AMB is a horizontal straight line touching the pulley at M. Angle SAB = 90° and angle TBA = 60°.
(a) Calculate (i) the obtuse angle SOT ; (ii) arc SRT ; (iii) |BT|
(b) Find, correct to the nearest cm, the length of the string. (Take \(\pi = \frac{22}{7}\)).
A surveyor standing at a point X sights a pole Y due east of him and a tower Z of a building on a bearing of 046°. After walking to a point W, a distance of 180m in the South- East direction, he observes the bearing of Z and Y to be 337° and 050° respectively.
(a) Calculate, correct to the nearest metre : (i) |XY| ; (ii) |ZW|
(b) If N is on XY such that XZ = ZN, find the bearing of Z from N.
Using a ruler and a pair of compasses only, construct (a) triangle QRT with |QR| = 8cm, |RT| = 6cm and |QT| = 4.5cm.
(b) a quadrilateral QRSP which has a common base QR with \(\Delta\)QRT such that QTP is a straight line, PQ || SR, |QP| = 9cm and |RS| = 4.5cm.
(i) Measure |PS| ; (ii) Find the perpendicular distance between RS and PQ ; (iii) What is QRSP?
(a) Copy and complete the table of values for the relation \(y = 5 – 7x – 6x^{2}\) for \(-3 \leq x \leq 2\).
| x | -3 | -2 | -1 | -0.5 | 0 | 1 | 2 |
| y | -28 | 6 | 5 |
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, draw the :
(i) graph of \(y = 5 – 7x – 6x^{2}\) ; (ii) line \(y = 3\) on the same axis.
(c) Use your graph to find the : (i) roots of the equation \(2 – 7x – 6x^{2} = 0\) ; (ii) maximum value of \(y = 5 – 7x – 6x^{2}\).
(a) A radio which a dealer bought for N6,000.00 and marked to give a profit of 30% was reduced in a sales by 10%. Find : (i) the final sales price ; (ii) the percentage profit.
(b) Solve the equation : \(2^{(2x + 1)} – 9(2^{x}) + 4 = 0\).
The third term of a Geometric Progression (G.P) is 360 and the sixth term is 1215. Find the
(a) common ratio;
(b) first term ;
(c) sum of the first four terms.
(a) A number is selected at random from each of the sets {2, 3, 4} and {1, 3, 5}. What is the probability that the sum of the two numbers will be less than 7 but greater than 3?
(b) 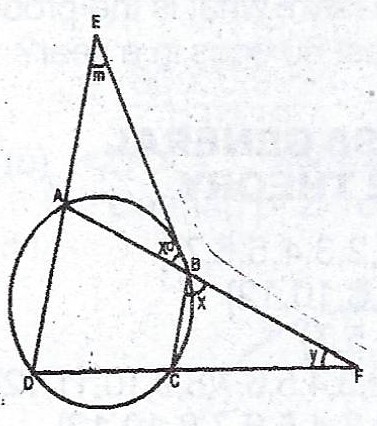
In the diagram, ABCD is a circle. DAE, CBE, ABF and DCF are straight lines. If y + m = 90°, find the value of x.
The area of a rectangular floor is 13.5m\(^{2}\). One side is 1.5m longer than the other.
(a) Calculate the dimensions of the floor ;
(b) If it costs N250.00 per square metre to carpet the floor and only N2,000.00 is available, what area of the floor can be covered with carpet?
(a) The value of the expression \(2Ax – Kx^{2}\) is 7 when x = 1 and 4 when x = 2. Find the values of the constants A and K.
(b) Solve the equation \(x^{2} – 3x – 1 = 0\), giving your answers correct to 1 decimal place.
(a) Given that \(\log_{10} 2 = 0.3010, \log_{10} 7 = 0.8451\) and \(\log_{10} 5 = 0.6990\), evaluate without using logarithm tables:
(i) \(\log_{10} 35\); (ii) \(\log_{10} 2.8\).
(b) Given that \(N^{0.8942} = 2.8\), use your result in (a)(ii) to find the value of N.
A, B and C are subsets of the universal set U such that : \(U = {0, 1, 2, 3,…, 12}; A = {x : 0 \leq x \leq 7}; B = {4, 6, 8, 10, 12}; C = {1 < y < 8}\), where y is a prime number.
(a) Draw a venn diagram to illustrate the information given above;
(b) Find: (i) \((B \cup C)’\); (ii) \(A’ \cap B \cap C\).
Arrange in ascending order of magnitude \(26_8, 36_7, and 25_9\)
- A. \(25_9 26_8 36_7\)
- B. \(26_8 25_9 36_7\)
- C. \(36_7 26_8 25_9\)
- D. \(36_7 25_9 26_8\)
The side of a square is increased from 20cm to 21cm. Calculate the percentage increase in its area
- A. 2.5%
- B. 9.3%
- C. 10.0%
- D. 10.25%
A trader makes a loss of 15% when selling an article. Find the ratio, selling price : cost price
- A. 3:20
- B. 3:17
- C. 17:20
- D. 20:23
Evaluate \(3.0\times 10^1 – 2.8\times 10^{-1}\)leaving the answer in standard form
- A. \(2\times 10^{-1}\)
- B. \(2\times 10^{2}\)
- C. \(2.972 \times 10^{1}\)
- D. \(2.972 \times 10^{2}\)
It is observed that \(1 + 3 = 2^2, 1 + 3 + 5 = 3^2, 1 + 3 + 5 + 7 = 4^2. \\If \hspace{1mm}1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = P^2 find\hspace{1mm}P\)
- A. 6
- B. 7
- C. 8
- D. 9
If P = {3, 7, 11, 13} and Q = {2, 4, 8, 16}, which of the following is correct
- A. \((P\cap Q)^l={2, 3, 4, 13}\)
- B. \(n(P\cup Q)=4\)
- C. \(P\cup Q = \emptyset\)
- D. \(P\cap Q = \emptyset\)
Three of the angles of a hexagon are each Xo. The others are each 3Xo. Find X
- A. 30o
- B. 40o
- C. 60o
- D. 80o
- E. 120o
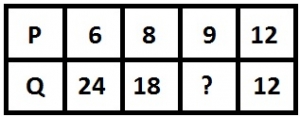
P varies inversely as Q. The table above shows the value of Q for some selected values of P
What is the missing value of Q in the table?
- A. 4
- B. 9
- C. 15
- D. 16
- E. 144


