(a) A number is selected at random from each of the sets {2, 3, 4} and {1, 3, 5}. What is the probability that the sum of the two numbers will be less than 7 but greater than 3?
(b) 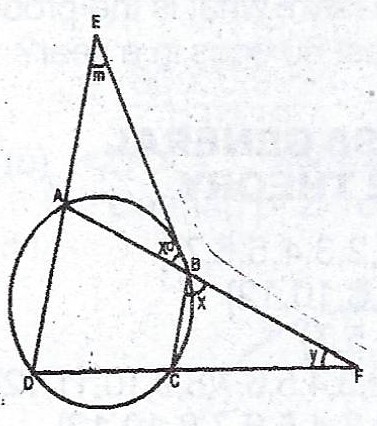
In the diagram, ABCD is a circle. DAE, CBE, ABF and DCF are straight lines. If y + m = 90°, find the value of x.
Explanation
(a)
| + | 1 | 3 | 5 |
| 2 | 3 | 5 | 7 |
| 3 | 4 | 6 | 8 |
| 4 | 5 | 7 | 9 |
Sample space = 9
Sum greater than 3 but less than 7 = {5, 4, 6, 5} = 4
P(sum greater than 3 but less than 7) = \(\frac{4}{9}\).
(b) Given that y + m = 90°
< ABE = x° (vertically opp. angles)
< BAD = (x + m)° (exterior angles)
< DCB = (x + y)° (exterior angles)
(x + m)° + (x + y)° = 180° (opp. angles of a cyclic quadrilateral)
(2x + y + m)° = 180°
(2x + 90) = 180
2x = 180 - 90 = 90°
x = 45°

