(a) Copy and complete the table of values for the relation \(y = 5 – 7x – 6x^{2}\) for \(-3 \leq x \leq 2\).
| x | -3 | -2 | -1 | -0.5 | 0 | 1 | 2 |
| y | -28 | 6 | 5 |
(b) Using a scale of 2cm to 1 unit on the x- axis and 2cm to 5 units on the y- axis, draw the :
(i) graph of \(y = 5 – 7x – 6x^{2}\) ; (ii) line \(y = 3\) on the same axis.
(c) Use your graph to find the : (i) roots of the equation \(2 – 7x – 6x^{2} = 0\) ; (ii) maximum value of \(y = 5 – 7x – 6x^{2}\).
Explanation
| x | -3 | -2 | -1 | -0.5 | 0 | 1 | 2 |
| y | -28 | -5 | 6 | 7 | 5 | -8 | -33 |
(b)(i) 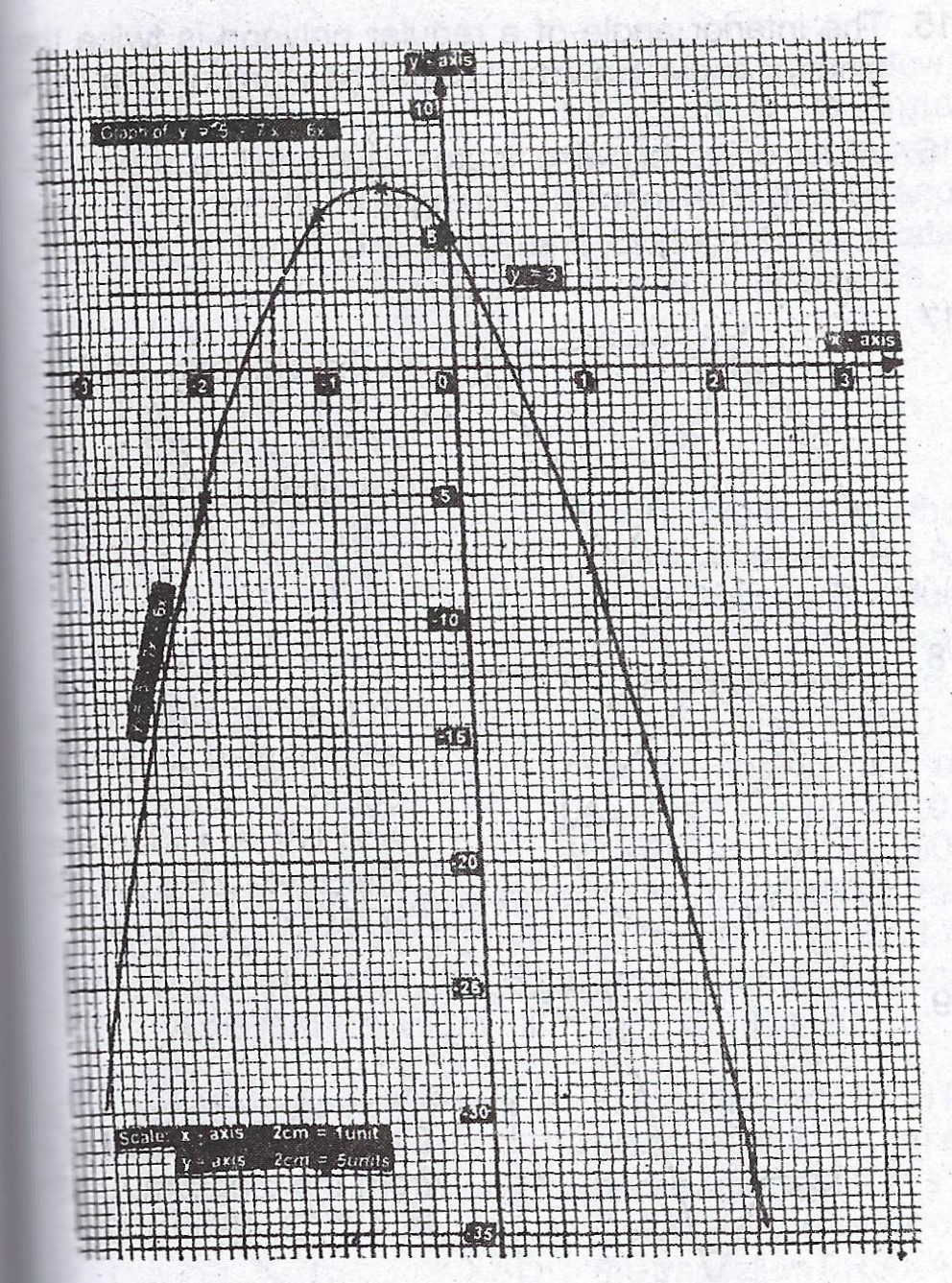
(c)(i) \(2 - 7x - 6x^{2} = 0\)
\(2 + 3 - 7x - 6x^{2} = 3\)
\(5 - 7x - 6x^{2} = 3\)
\(\therefore \text{the roots at y = 3 are } x = -1.4; 0.2\)
(ii) Maximum value of \(y = 5 - 7x - 6x^{2}\) is y = 7.

