A surveyor standing at a point X sights a pole Y due east of him and a tower Z of a building on a bearing of 046°. After walking to a point W, a distance of 180m in the South- East direction, he observes the bearing of Z and Y to be 337° and 050° respectively.
(a) Calculate, correct to the nearest metre : (i) |XY| ; (ii) |ZW|
(b) If N is on XY such that XZ = ZN, find the bearing of Z from N.
Explanation
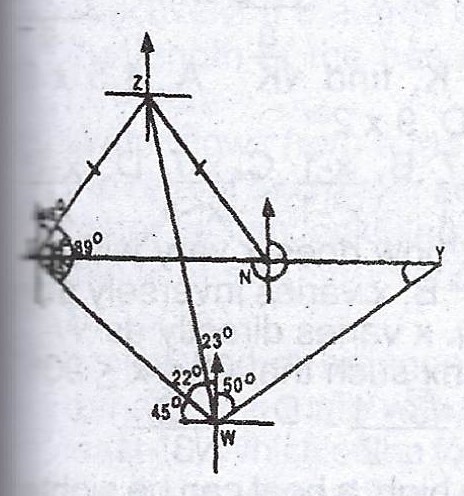
XWZ = 90° - (45° + 23°) = 22°
WYX = 180° - (45° + 95°) = 40°
< XZW = 180° - (89° + 22°) = 69°
(a)(i) \(\frac{XY}{\sin 95} = \frac{180}{\sin 40°}\)
\(XY = \frac{180 \sin 95}{\sin 40} = 278.96m\)
\(\approxeq 279m\)
(ii) \(\frac{ZW}{\sin 89°} = \frac{180}{\sin 69°}\)
\(ZW = \frac{180 \sin 89°}{\sin 69°} = 192.76m\)
\(\approxeq 193m\)
(b) < ZNX = <ZXN (base angles of an isosceles triangle)
= 44°^.
\(\therefore\) Bearing of Z from N = 270° + 44° = 314°.

