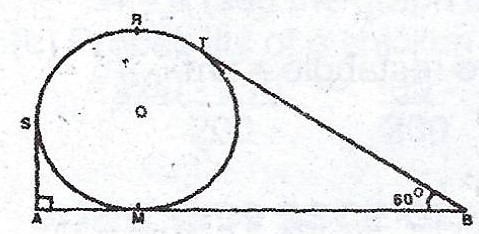
In the diagram, ASRTB represents a piece of string passing over a pulley of radius 10cm in a vertical plane. O is the centre of the pulley and AMB is a horizontal straight line touching the pulley at M. Angle SAB = 90° and angle TBA = 60°.
(a) Calculate (i) the obtuse angle SOT ; (ii) arc SRT ; (iii) |BT|
(b) Find, correct to the nearest cm, the length of the string. (Take \(\pi = \frac{22}{7}\)).
Explanation
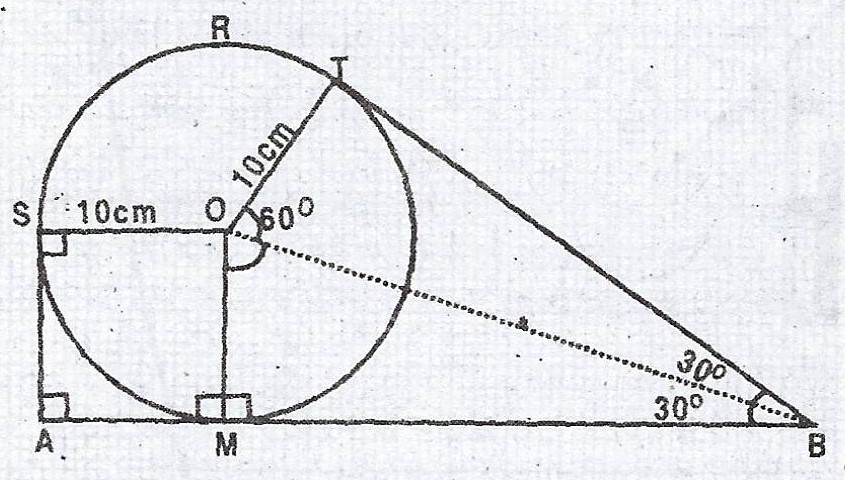
(a)(i) < ASO = < AMO = 90° (radius to a tangent)
< SOM = 360° - (3 x 90°) (sum of angles of a rectangle)
= 90°.
\(\therefore\) obtuse < SOT = 360° - (90° + 60° + 60°) = 150°.
(ii) Arc SRT = \(\frac{150°}{360°} \times 2\pi r\)
= \(\frac{150}{360} \times 2 \times \frac{22}{7} \times 10 = \frac{550}{21}\)
= \(26.19cm\)
(iii) \(\tan 60° = \frac{TB}{10}\)
\(TB = 10\tan 60° = 17.32cm\)
(b) Length of the string ASRTB = AS + arc SRT + TB
= 10cm + 26.19cm + 17.32cm
= 53.51cm \(\approxeq\) 54cm.

