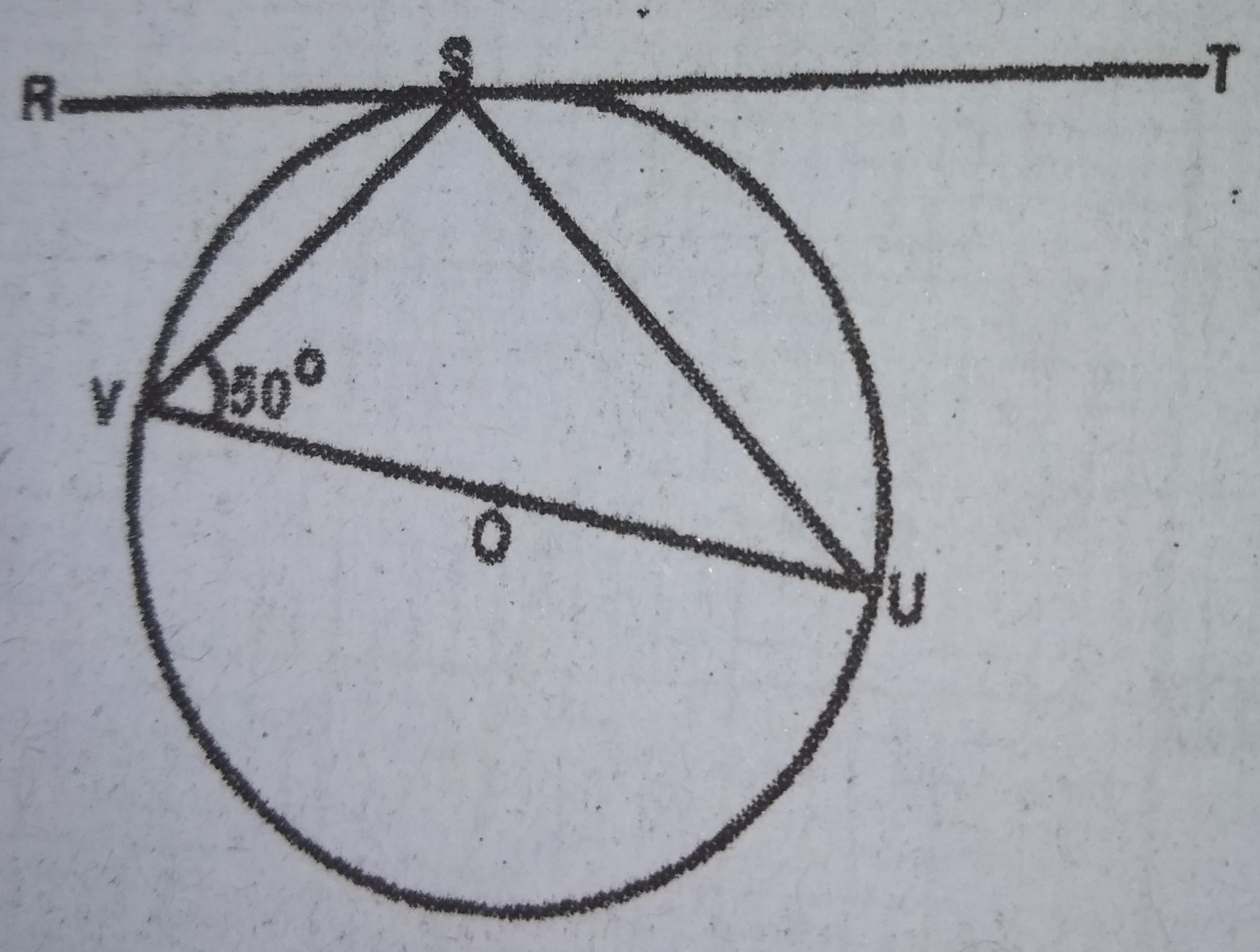
In the diagram above, RST is a tangent to circle VSU center O ∠SVU = 50° and UV is a diameter. Calculate ∠RSV.
- A. 90°
- B. 50°
- C. 45°
- D. 40°
(a) Copy and complete the following table of values for \(y = 9 \cos x + 5 \sin x\) to one decimal place.
| x | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° |
| y | 10.3 | -0.2 | -5.3 | -10.3 |
(b) Using a scale of 2cm to 30° on the x- axis and 2 cm to 1 unit on the y- axis, draw the graph of \(y = 9 \cos x + 5 \sin x\) for \(0° \leq x \leq 210°\).
(c) Use your graph to solve the equation: (i) \(9\cos x + 5\sin x = 0\); (ii) \(9\cos x+ 5\sin x = 3.5\), correct to the nearest degree.
(d) Find the maximum value of y correct to one decimal place.
(a) A shop owner marked a shirt at a price to enable him to make a gain of 20%. During a special sales period, the shirt was sold at 10% reduction to a customer at N864.00. What was the original cost to the shop owner?
(b) A rectangular lawn of length (x + 5) metres is (x – 2) metres wide. If the diagonal is (x + 6) metres, find ;
(i) the value of x ; (ii) the area of lawn.
On a graph sheet, using a scale of 2cm to 2 units on both axes,
(a) Draw the straight line joining points P(-5, 3) and Q(2, 3);
(b) construct the locus L of points equidistant from P and Q;
(c) by construction, locate points R and S on L, such that PRQS forms a rhombus of sides 5cm;
(d) find : (i) coordinates of R and S; (ii) area of the rhombus in cm\(^{2}\).
The cost of maintaining a school is partly constant and partly varies as the number of pupils. With 50 pupils, the cost is $15,705.00 and with 40 pupils, it is $13,305.00.
(a) Find the cost when there are 44 pupils.
(b) If the fee per pupil is $360.00, what is the least number of pupils for which the school can run without a loss?
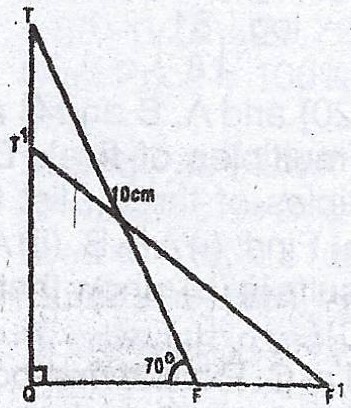
In the diagram, a ladder TF, 10 metres long is placed against a wall at an angle of 70° to the horizontal.
(a) How high up the wall, correct to the nearest metre, does the ladder reach?
(b) If the foot (F) of the ladder is pulled from the wall to F\(^{1}\) by 1 metre, (i) how far, correct to 2 significant figures, does the top T slide down the wall to T\(^{1}\).
(ii) Calculate, correct to the nearest degree, \(QF^{1}T^{1}\).
(a) Given that \(\sin(A + B) = \sin A \cos B + \cos A \sin B\). Without using mathematical tables or calculator, evaluate \(\sin 105°\), leaving your answer in the surd form.
(You may use 105° = 60° + 45°)
(b) The houses on one side of a particular street are assigned odd numbers, starting from 11. If the sum of the numbers is 551, how many houses are there?
(c) The 1st and 3rd terms of a Geometric Progression (G.P) are \(2\) and \(\frac{2}{9}\) respectively. Find :
(i) the common difference ; (ii) the 5th term.
(a) A cylindrical pipe is 28 metres long. Its internal radius is 3.5 cm and external radius 5 cm. Calaulate : (i) the volume, in cm\(^{3}\), of metal used in making the pipe ; (ii) the volume of water in litres that the pipe can hold when full, correct to 1 decimal place. [Take \(\pi = \frac{22}{7}\)]
(b) 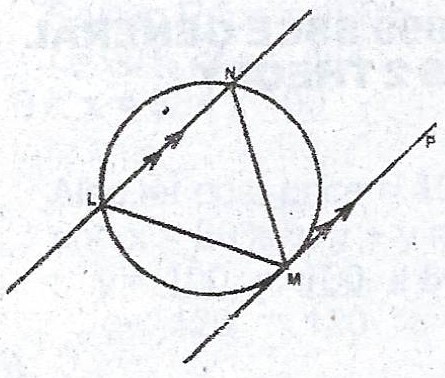 In the diagram, MP is a tangent to the circle LMN at M. If the chord LN is parallel to MP, show that the triangle LMN is isosceles.
In the diagram, MP is a tangent to the circle LMN at M. If the chord LN is parallel to MP, show that the triangle LMN is isosceles.
The table gives the frequency distribution of marks obtained by a group of students in a test.
| Marks | 3 | 4 | 5 | 6 | 7 | 8 |
| Frequency | 5 | x – 1 | x | 9 | 4 | 1 |
If the mean is 5,
(a) Calculate the value of x;
(b) Find the : (i) mode ; (ii) median of the distribution.
(c) If one of the students is selected at random, find the probability that he scored at least 7 marks.
(a) Solve the simultaneous equations 3y – 2x = 21 ; 4y + 5x = 5.
(b) Six identical cards numbered 1 – 6 are placed face down. A card is to be picked at random. A person wins $60.00 if he picks the card numbered 6. If he picks any of the other cards, he loses $10.00 times the number on the card. Calculate the probability of (i) losing ; (ii) losing $20.00 after two picks.
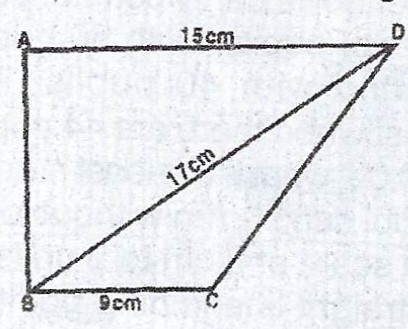
In the diagram, ABCD is a trapezium in which \(AD \parallel BC\) and \(< ABC\) is a right angle. If |AD| = 15 cm, |BD| = 17 cm and |BC| = 9 cm, calculate :
(a) |AB| ;
(b) the area of the triangle BCD ;
(c) |CD| ;
(d) perimeter of the trapezium.
ABC is a triangle, right-angled at C. P is the mid-point of AC, < PBC = 37° and |BC| = 5 cm. Calculate :
(a) |AC|, correct to 3 significant figures ;
(b) < PBA.
(a) If \(\varepsilon\) is the set \({1, 2, 3,…, 19, 20}\) and A, B and C are subsets of \(\varepsilon\) such that A = { multiples of five}, B = {multiples of four} and C = {multiples of three}, list the elements of (i) A ; (ii) B ; (iii) C ;
(b) Find : (i) \(A \cap B\) ; (ii) \(A \cap C\) ; (iii) \(B \cup C\).
(c) Using your results in (b), show that \((A \cap B) \cup (A \cap C) = A \cap (B \cup C)\).
(a) Simplify \((\frac{4}{25})^{-\frac{1}{2}} \times 2^{4} \div (\frac{15}{2})^{-2}\)
(b) Evaluate \(\log_{5} (\frac{3}{5}) + 3 \log_{5} (\frac{5}{2}) – \log_{5} (\frac{81}{8})\).

In the diagram, CDE is a triangle, ABEF is cyclic quadrilateral, AB||CD, ∠BAF = 65o and ∠AFE = 85o calculate ∠CDE
- A. 20o
- B. 30o
- C. 50o
- D. 65o
The sides of a right angle triangle in ascending order of magnitude are 8cm, (x-2)cm and x cm. Find x
- A. 16
- B. 17
- C. 34
- D. 90
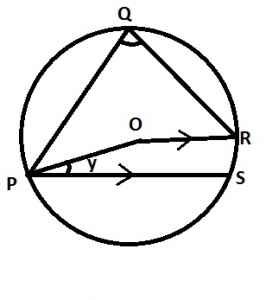
In the diagram, O is the centre of the circle ∠PQR = 75o, ∠OPS = yo and \(\bar{OR}\) is parallel to \(\bar{PS}\). Find y
- A. 15
- B. 30
- C. 45
- D. 75
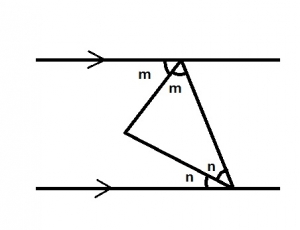
Which of the following statements is true from the diagram above?
- A. m + n = 90o
- B. m = n
- C. n > 45o
- D. m < 45o
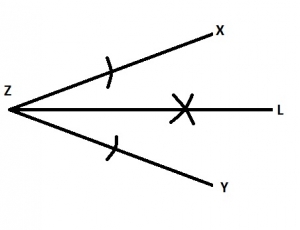
Describe the locus L shown in the diagram below
- A. Locus of points equidistant from X and Y
- B. Locus of points equidistant from X and Z
- C. Locus of points equidistant from \(\bar{ZX}\) and \(\bar{ZY}\)
- D. Locus of points equidistant from \(\bar{XY}\) and \(\bar{ZY}\)
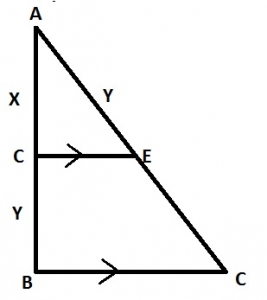
In the diagram, DE||BC, |AD| = x cm and |DB| = |AE| = ycm. Find |CE| in terms of x and y
- A. x
- B. \(\frac{x^2}{y}\)
- C. \(\frac{y}{x^2}\)
- D. \(\frac{y^2}{x}\)
Solve the inequality 2x + 3 < 5x
- A. \(x>1\)
- B. \(x<\frac{3}{7}\)
- C. \(x>\frac{3}{7}\)
- D. \(x>-1\)


