ABC is a triangle, right-angled at C. P is the mid-point of AC, < PBC = 37° and |BC| = 5 cm. Calculate :
(a) |AC|, correct to 3 significant figures ;
(b) < PBA.
Explanation
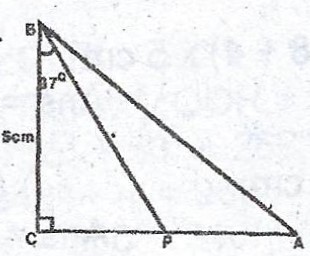
Let |PC| = x cm; Hence, |AC| = 2x cm
\(\tan 37° = \frac{x}{5}\)
\(x = 5 \tan 37 \)
\(x = 3.768 cm\)
\(\therefore |AC| = 2 \times 3.768\)
= \(7.536 cm\)
\(\approxeq 7.54 cm\) (3 sig. figs)
(b) From \(\Delta ABC\),
\(\tan < ABC = \frac{7.536}{5} = 1.5072\)
\(< ABC = \tan^{-1} (1.5072) = 56.436°\)
\(\therefore < PBA = < ABC - < PBC\)
= \(56.436° - 37°\)
= \(19.436° \approxeq 19.44°\)

