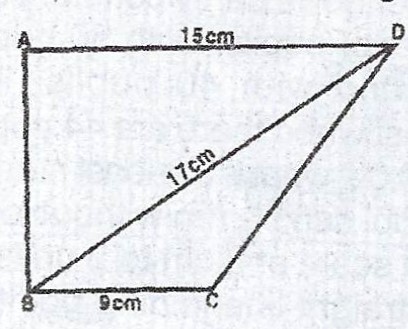
In the diagram, ABCD is a trapezium in which \(AD \parallel BC\) and \(< ABC\) is a right angle. If |AD| = 15 cm, |BD| = 17 cm and |BC| = 9 cm, calculate :
(a) |AB| ;
(b) the area of the triangle BCD ;
(c) |CD| ;
(d) perimeter of the trapezium.
Explanation
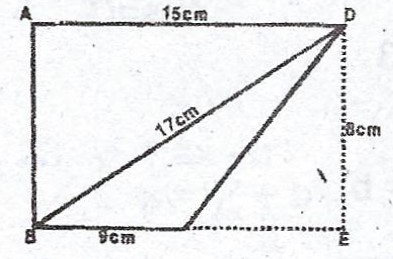
(a) \(|AB| = \sqrt{|BD|^{2} - |AD|^{2}}\)
= \(\sqrt{17^{2} - 15^{2}} = \sqrt{289 - 225}\)
= \(\sqrt{64} = 8 cm\)
(b) Area of triangle BCD = \(\frac{1}{2} \times 9 \times 8 \)
= \(36 cm^{2}\)
(c) \(|EC| = 6 cm\)
\(|CD| = \sqrt{8^{2} + 6^{2}} = \sqrt{100}\)
= 10 cm.
(d) Perimeter of the trapezium = 15 cm + 8 cm + 9 cm + 10 cm
= 42 cm.

