(a) Two places X and Y on the equator are on longitudes 67°E and 123°E respectively. (i) What is the distance between them along the equator? (ii) How far from the North pole is X? [Take \(\pi = \frac{22}{7}\) and radius of earth = 6400km].
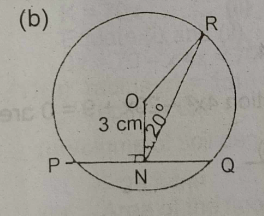
(b) SEE FIGURE B above, In the diagram, PQR is a circle centre O. N is the mid-point of chord PQ. |PQ| = 8cm, |ON| = 3cm and < ONR = 20°. Calculate the size of < ORN to the nearest degree.
(a) The first term of an Arithmetic Progression (A.P) is 8. The ratio of the 7th term to the 9th term is 5 : 8. Calculate the common difference of the progression.
(b) A sphere of radius 2 cm is of mass 11.2g. Find (i) the volume of the sphere ; (ii) the density of the sphere ; (iii) the mass of a sphere of the same material but with radius 3cm. [Take \(\pi = \frac{22}{7}\)].
(a) A cylindrical well of radius 1 metre is dug out to a depth of 8 metres. (i) calculate, in m\(^{3}\), the volume of soil dug out ; (ii) if the soil is used to raise the level of rectangular floor of a room 4m by 12m, calculate, correct to the nearest cm, the thickness of the new layer of soil. [Take \(\pi = \frac{22}{7}\)].
(b) see figure b above.
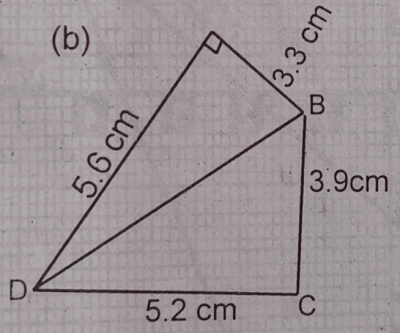
The diagram shows a quadrilateral ABCD in which < DAB is a right-angle. |AB| = 3.3 cm, |BC| = 3.9 cm, |CD| = 5.6 cm. (i) find the length of BD. (ii) show that < BCD = 90°.
(a) A surveyor walks 100m up a hill which slopes at an angle of 24° to the horizontal. Calculate, correct to the nearest metre, the height through which he rises.
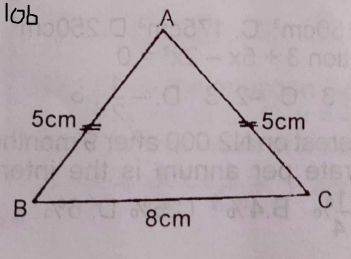
(b) Use Figure 10b above to answer the question below.
In the diagram, ABC is an isosceles triangle. |AB| = |AC| = 5 cm, and |BC| = 8 cm. Calculate, correct to the nearest degree, < BAC.
(c) Two boats, 70 metres apart and on opposite sides of a light-house, are in a straight line with the light-house. The angles of elevation of the top of the light-house from the two boats are 71.6° and 45°. Find the height of the light-house. [Take tan 71.6° = 3].
(a) The mean of 1, 2, x, 11, y, 14, arranged in ascending order, is 8 and the median is 9. Find the values of x and y.
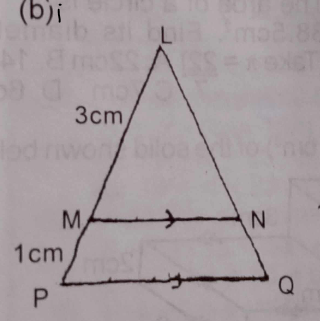
(b) Use the figure above to answer the question(i) below.
(i) In the diagram, MN || PQ, |LM| = 3cm and |LP| = 4cm. If the area of \(\Delta\) LMN is 18\(cm^{2}\), find the area of the quadrilateral MPQN.
(a) Copy and complete the following table of values for the relation \(y = x^{2} – 2x – 5\)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | -2 | -6 | -2 | 3 | 10 |
(b) Draw the graph of the relation \(y = x^{2} – 2x – 5\); using a scale of 2 cm to 1 unit on the x- axis, and 2 cm to 2 units on the y- axis.
(c) Using the same axes, draw the graph of \(y = 2x + 3\).
(d) Obtain in the form \(ax^{2} + bx + c = 0\) where a, b and c are integers, the equation which is satisfied by the x- coordinate of the points of intersection of the two graphs.
(e) From your graphs, determine the roots of the equation obtained in (d) above.
(a) A man earns N150,000 per annum. He is allowed a tax free pay on N40,000. If he pays 25 kobo in the naira as tax on his taxable income, how much has he left?
(b) A bookshop has 650 copies of a book for sale. The books were marked at N75 per copy in order to make a profit of 30%. A bookseller bought 300 copies at 5% discount. If the remaining copies are sold at N75 each, calculate the percentage profit the bookshop would make on the whole.
(a)
| Limes | Apples | |
| Good | 10 | 8 |
| Bad | 6 | 6 |
The table shows the number of limes and apples of the same size in a bag. If two of the fruits are picked at random, one at a time, without replacement, find the probability that : (i) both are good limes ; (ii) both are bad fruits ; (iii) one is a good apple and the other a bad lime.
(b) Solve the equation \(\log_{3} (4x + 1) – \log_{3} (3x – 5) = 2\).
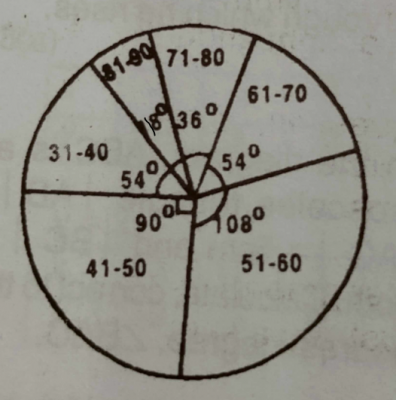
The pie chart above shows the distribution of marks scored by 200 pupils in a test.
(a) How many pupils scored : (i) between 41 and 50 marks? ; (ii) above 80 marks?
(b) What fraction of the pupils scored at most 50 marks?
(c) What is the modal class?
Using ruler and a pair of compasses only,
(a) construct \(\Delta PQR\) such that |PQ| = 7 cm, |PR| = 6 cm and < PQR = 60°.
(b) locate point M, the mid-point of PQ.
(c) Measure < RMQ.
(a) Given the expression \(y = ax^{2} – bx – 12\) , find the values of x when a = 1, b = 2 and y = 3.
(b) If \(\sqrt{x^{2} + 1} = \frac{5}{4}\), find the positive value of x.
(a) Given that cos x = 0.7431, 0° < x < 90°, use tables to find the values of : (i) 2sin x ; (ii) tan\(\frac{x}{2}\).
(b) The interior angles of a pentagon are in ratio 2 : 3: 4: 4: 5. Find the value of the largest angle.
(a) Evaluate and express your answer in standard form : \(\frac{4.56 \times 3.6}{0.12}\)
(b) Without using mathematical tables or calculator, evaluate \((73.8)^{2} – (26.2)^{2}\).
(c) Simplify \(\sqrt{1\frac{19}{81}}\), expressing your answer in the form \(\frac{a}{b}\) where a and b are positive integers.
If the simple interest on N2000 after 9 months is N60, at what rate per annum is the interest charged?
- A. \(2\frac{1}{4}\)%
- B. 4%
- C. 5%
- D. 6%
Solve the equation 3 + 5x – 2x2 = 0
- A. \(-\frac{1}{2},-3\)
- B. 2, 3
- C. -2, 3
- D. \(-\frac{1}{2},3\)
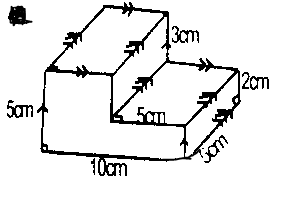
Find the volume (in cm\(^3\)) of the solid shown above
- A. 100cm3
- B. 150cm3
- C. 175cm3
- D. 250cm3
The area of a circle is 38.5cm2. Find its diameter [take \(\pi = \frac{22}{7}\)]
- A. 22cm
- B. 14cm
- C. 7cm
- D. 6cm
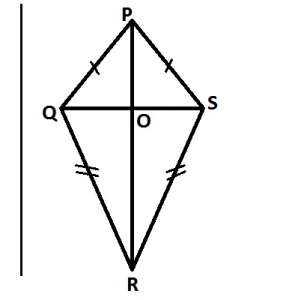
In the diagram, |PQ| = |PS| Which of the following statements is true?
- A. ∠QPS = QRS
- B. |PO| = |RO|
- C. QR||PS
- D. ∠PQR=∠PSR
The arc of a circle 50 cm long, subtends angle of 75° at the center of the circle. Find correct to 3 significant figures, the radius of the circle. Take \(\pi = \frac{22}{7}\)
- A. 8.74cm
- B. 38.2cm
- C. 61.2cm
- D. 76.4cm
The length of the parallel sides of a trapezium are 5cm and 7cm. If its area is 120cm\(^2\), find the perpendicular distance between the parallel sides
- A. 5.0cm
- B. 6.9cm
- C. 10.0cm
- D. 20.0cm
A tap leaks at the rate of 2cm\(^3\) per seconds. How long will it take the tap to fill a container of 45 liters capacity? (1 liters = 1000cm\(^3\))
- A. 8 hours
- B. 6hr 15min
- C. 4hr 25min
- D. 3hr


