(a) The mean of 1, 2, x, 11, y, 14, arranged in ascending order, is 8 and the median is 9. Find the values of x and y.
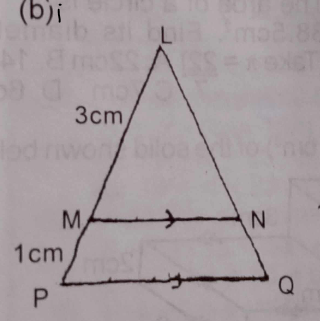
(b) Use the figure above to answer the question(i) below.
(i) In the diagram, MN || PQ, |LM| = 3cm and |LP| = 4cm. If the area of \(\Delta\) LMN is 18\(cm^{2}\), find the area of the quadrilateral MPQN.
Explanation
(a) Mean \(\bar{x} = \frac{\sum x}{n} = 8\)
\(\frac{1 + 2 + x + 11 + y + 14}{6} = 8\)
\(28 + x + y = 48 \implies x + y = 20 .... (1) \)
The middle numbers are x and 11 therefore, \(\frac{x + 11}{2} = 9\)
\(x + 11 = 18 \implies x = 18 - 11 = 7\)
Putting x = 7 in (1),
\(7 + y = 20 \implies y = 20 - 7 = 13\)
(x, y) = (7, 13).
(b) \(\frac{LM}{LP} = \frac{3}{4}\)
\(\frac{\text{Area of LMN}}{\text{Area of LPQ}} = \frac{3^{2}}{4^{2}}\)
Area of \(\Delta\) LPQ = \(\frac{16}{9} \times 18 = 32 cm^{2}\)
\(\therefore \text{Area of quadrilateral MPQN} = 32 - 18 = 14 cm^{2}\)

