(a) A surveyor walks 100m up a hill which slopes at an angle of 24° to the horizontal. Calculate, correct to the nearest metre, the height through which he rises.
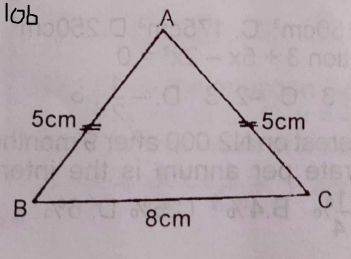
(b) Use Figure 10b above to answer the question below.
In the diagram, ABC is an isosceles triangle. |AB| = |AC| = 5 cm, and |BC| = 8 cm. Calculate, correct to the nearest degree, < BAC.
(c) Two boats, 70 metres apart and on opposite sides of a light-house, are in a straight line with the light-house. The angles of elevation of the top of the light-house from the two boats are 71.6° and 45°. Find the height of the light-house. [Take tan 71.6° = 3].
Explanation
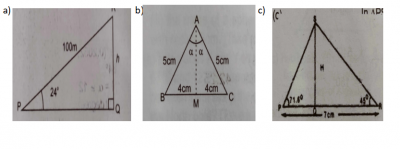
(a) see figure a above \(\frac{h}{100} = \sin 24\)
\(h = 100 \sin 24\)
= \(100 \times 0.4067\)
= \(40.67m\)
(b) see figure b above \(\sin \alpha = \frac{4}{5} = 0.8\)
\(\alpha = \sin^{-1} (0.8) = 53.13°\)
\(< BAC = 2 \theta = 2(53.13°)\)
= \(106.26°\)
\(\approxeq 106°\) (to the nearest degree).
(c) See Figure C above
In \(\Delta PSQ\),
\(\frac{h}{PQ} = \tan 71.6\)
\(PQ = \frac{h}{\tan 71.6}\)
In \(\Delta QSR\),
\(\frac{h}{QR} = \tan 45\)
\(QR = \frac{h}{\tan 45}\)
\(PR = PQ + QR\)
\(\frac{h}{3} + h = 70 \implies \frac{4}{3}h = 70\)
\(h = \frac{70 \times 3}{4} = 52.5m\)

