(a) A cylindrical well of radius 1 metre is dug out to a depth of 8 metres. (i) calculate, in m\(^{3}\), the volume of soil dug out ; (ii) if the soil is used to raise the level of rectangular floor of a room 4m by 12m, calculate, correct to the nearest cm, the thickness of the new layer of soil. [Take \(\pi = \frac{22}{7}\)].
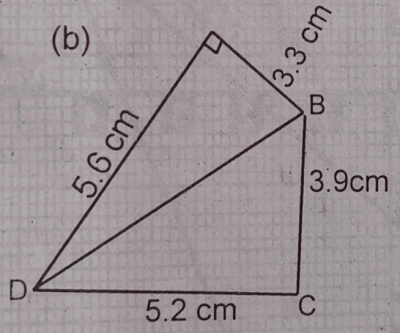
(b) see figure b above.
The diagram shows a quadrilateral ABCD in which < DAB is a right-angle. |AB| = 3.3 cm, |BC| = 3.9 cm, |CD| = 5.6 cm. (i) find the length of BD. (ii) show that < BCD = 90°.
Explanation
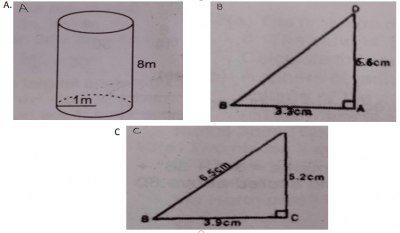
(a) See Figure A above. (i) r = 1m, h = 8m.
\(V = \pi r^{2} h = \frac{22}{7} \times 1^{2} \times 8\)
= \(\frac{176}{7}\)
= \(25.14 m^{3}\)
(ii) \(V = L \times B \times H\)
\(\frac{176}{7} = 4 \times 12 \times h\)
\(h = \frac{176}{7} \div 48\)
\(h = \frac{11}{21}m\)
= \(\frac{1100}{21} cm = 52.38 cm\)
\(\approxeq 52 cm\) (nearest whole number)
(b)(i) see figure B. \(3.3^{2} + 5.6^{2} = BD^{2}\)
\(BD = \sqrt{3.3^{2} + 5.6^{2}}\)
= \(\sqrt{10.89 + 31.36}\)
= \(\sqrt{42.25} = 6.5 cm\)
(ii) See Figure C
If < BCD is right-angled, then Pythagoras rule holds true.
\(BD^{2} = 5.2^{2} + 3.9^{2} = 27.04 + 15.21\)
= \(42.25\)
\(BD = \sqrt{42.25} = 6.5 cm\)
Hence, \(\Delta BCD\) is right-angled.

