(a) Two places X and Y on the equator are on longitudes 67°E and 123°E respectively. (i) What is the distance between them along the equator? (ii) How far from the North pole is X? [Take \(\pi = \frac{22}{7}\) and radius of earth = 6400km].
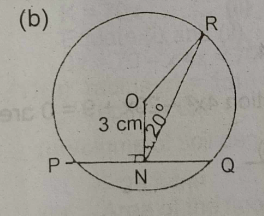
(b) SEE FIGURE B above, In the diagram, PQR is a circle centre O. N is the mid-point of chord PQ. |PQ| = 8cm, |ON| = 3cm and < ONR = 20°. Calculate the size of < ORN to the nearest degree.
Explanation
(a) SEE FIGURE A above., Longitude difference = 123° - 67° = 56°
(i) Distance between X and Y along the equator = \(\frac{56}{360} \times 2 \times \frac{22}{7} \times 6400 \cos 0\)
= \(\frac{56}{360} \times 2 \times \frac{22}{7} \times 6400\)
= \(6257.78km \approxeq 6258km\)
(ii) Latitude difference = 90°
Distance from the North pole = \(\frac{90}{360} \times 2 \times \frac{22}{7} \times 6400\)
= \(10057.14km \approxeq 10057km\)
(b) SEE FIGURE B above,.,
\(OP^{2} = PN^{2} + ON^{2}\)
\(4^{2} + 3^{2} = 25\)
\(OP = \sqrt{25} = 5cm\)
\(OP = OR = 5cm\)
\(\Delta NOR = scalene\)
\(\frac{OR}{\sin 20} = \frac{3}{\sin < ORN}\)
\(\frac{5}{\sin 20} = \frac{3}{\sin < ORN}\)
\(\sin < ORN = \frac{3 \times \sin 20}{5}\)
\(\sin < ORN = 0.2052\)
\(< ORN = \sin^{-1} (0.2052)\)
\(< ORN = 11.84° \approxeq 12°\)

