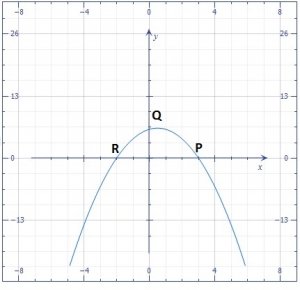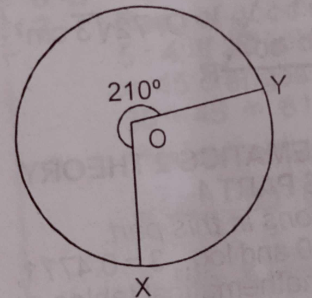
In the diagram above, O is the centre of the circle. Reflex angle XOY = 210º and the length of the minor arc is 5.5m. Find, correct to the nearest metre the length of major arc.
- A. 8m
- B. 9m
- C. 10m
- D. 13m
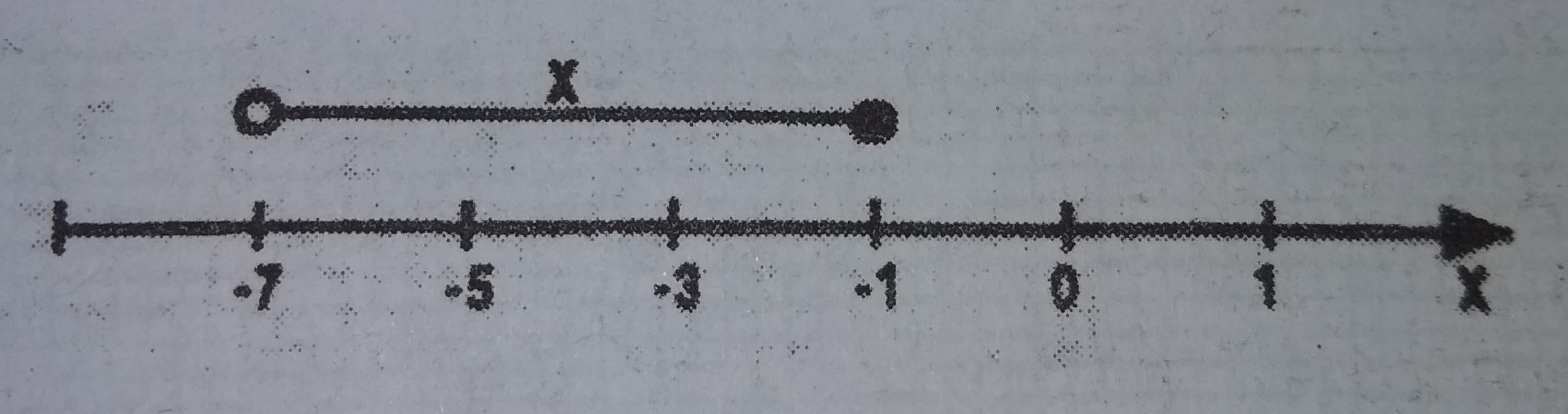
The number line represents
- A. 0 > x \(\geq\) -7
- B. -7 \(\leq\) x < -1
- C. -7 < x \(\leq\) -1
- D. -7 < x < -1
(a) A boy blew his rubber balloon to a spherical shape. The balloon burst when its diameter was 15 cm. Calculate, correct to the nearest whole number, the volume of air in the balloon at the point of bursting. [Take \(\pi = \frac{22}{7}\)]
(b) A point X is on latitude 28°N and longitude 105°W. Y is another point on the same latitude as X but on longitude 35°E. (i) Calculate, correct to three significant figures, the distance between X and Y along latitude 28°N ; (ii) How far is X from the equator? [Take \(\pi = \frac{22}{7}\) and radius of the earth = 6,400km].
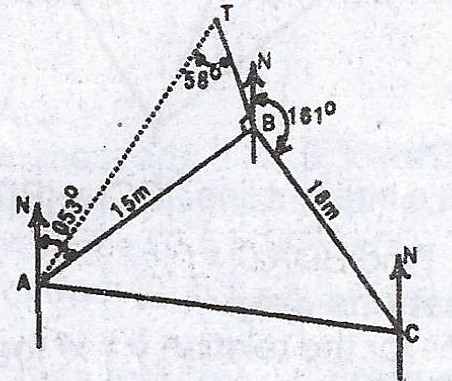In the diagram, three points A, B and C are on the same horizontal ground. B is 15m from A, on a bearing of 053°, C is 18m from B on a bearing of 161°. A vertical pole with top T is erected at B such that < ATB = 58°. Calculate, correct to three significant figures,
(a) the length of AC.
(b) the bearing of C from A ;
(c) the height of the pole BT.
(a) The roots of the equation \(2x^{2} + (p + 1)x + 9 = 0\), are 1 and 3, where p and q are constants. Find the values of p and q.
(b) The weight of an object varies inversely as the square of its distance from the centre of the earth. A small satellite weighs 80kg on the earth’s surface. Calculate, correct to the nearest whole number, the weight of the satellite when it is 800km above the surface of the earth. [Take the radius of the earth as 6,400km].
(a) The probabilities that three boys pass an examination are \(\frac{2}{3}, \frac{5}{8}\) and \(\frac{3}{4}\) respectively. Find the probability that :
(i) all three boys pass ; (ii) none of the boys pass ; (iii) only two of the boys pass.
(b) A shop-keeper marks a television set for sale at N36,000 so as to make a profit of 20% on the cost price. When he sells it, he allows a discount of 5% of the marked price. Calculate the actual percentage profit.
(a) In a market survey, 100 traders sell fruits, 40 sell apples, 46 oranges, 50 mangoes, 14 apples and oranges, 15 apples and mangoes and 10 sell the three types of fruits. Each of the 100 traders sells at least one of the three fruits.
(i) Represent the information in a Venn diagram ; (ii) Find the number that sell oranges and mangoes only.
(b) Find the value of x for which \(312_{four} + 52_{x} = 96_{ten}\)
The number of child births recorded in 50 maternity centres of a local government in August 1993 are as follows :
50 99 81 86 69 85 93 63 92 65 77 74 76 71 90 74 81 94 67 75 95 81 68 105 99 68 75 75 76 73 79 74 80 69 74 62 74 80 79 68 79 75 75 71 83 75 80 85 81 82
(a) Construct a frequency distribution table, using class intervals 45 – 54, 55 – 64, etc.
(b) Draw the histogram for the distribution
(c) Use your histogram to estimate the mode.
(d) Calculate the mean number of births.
(a) Draw the table of values for the relation \(y = x^{2}\) for the interval \(-3 \leq x \leq 4\).
(b) Using a scale of 2 cm to 1 unit on the x- axis and 2 cm to 2 units on the y- axis, draw the graphs of : (i) \(y = x^{2}\) ; (ii) \(y = 2x + 3\) for \(-3 \leq x \leq 4\).
(c) Use your graph to find : (i) the roots of the equation \(x^{2} = 2x + 3\) ; (ii) the gradient of \(y = x^{2}\) at x = -2.
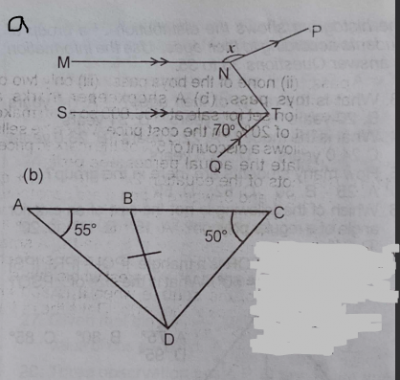
(a) see figure a above, In the diagram, MN || ST, NP || QT and < STQ = 70°. Find x.
(b) see figure b above, In the diagram above, AC is a straight line, |BC| = |BD|, \(\stackrel\frown{BCD} = 50°\) and \(\stackrel\frown{BAD} = 55°\). Find \(\stackrel\frown{BDA}\).
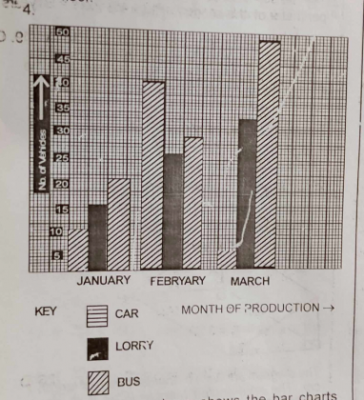
The diagram above shows the bar charts representing the number of vehicles manufactured by a company in January, February and March, 1992.
(a) How many vehicles were produced in February?
(b) What fraction of the vehicles manufactured in February were cars?
(c) How many buses were produced altogether from January to March, 1992?
(d) What is the ratio in the lowest term of the number of lorries produced in February to that in March?
The sides of a rectangular floor are xm and (x + 7)m. The diagonal is (x + 8)m. Calculate, in metres :
(a) the value of x ;
(b) the area of the floor.
(a) Simplify : \(\frac{1}{3^{5n}} \times 9^{n – 1} \times 27^{n + 1}\)
(b) The sum of the ages of a woman and her daughter is 46 years. In 4 years’ time, the ratio of their ages will be 7 : 2. Find their present ages.
Given that \(\log_{10} 2 = 0.3010\) and \(\log_{10} 3 = 0.4771\), calculate without using mathematical tables or calculator, the value of :
(a) \(\log_{10} 54\) ;
(b) \(\log_{10} 0.24\).
Given that P = {b, d, e, f} and Q = {a, c, f, g} are subsets of the universal set U = {a,b, c, d, e, f, g}. Find P’ ∩ Q
- A. {a,c}
- B. {a, c, d, g}
- C. {c, d, g}
- D. {a, c, g}
The variance of a given distribution is 25. What is the standard deviation?
- A. 125
- B. 75
- C. 25
- D. 5
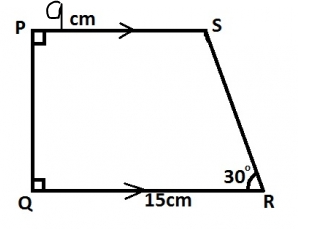
PQRS is a trapezium in which |PS| = 9cm, |QR| = 15cm, |PQ| = \(2\sqrt{3}, \angle PQR = 90^o and \angle QRS = 30^o\). Calculate the area of the trapezium
- A. \(24\sqrt{3} cm^2\)
- B. \(36\sqrt{3} cm^2\)
- C. \(42\sqrt{3} cm^2\)
- D. \(72\sqrt{3} cm^2\)
A solid cylinder of radius 7cm is 10 cm long. Find its total surface area.
- A. \(70\pi cm^2\)
- B. \(189\pi cm^2\)
- C. \(210\pi cm^2\)
- D. \(238\pi cm^2\)
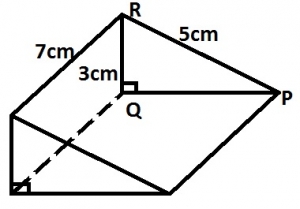
The diagram shows a triangular prism of length 7cm. The right – angled triangle PQR is a cross section of the prism |PR| = 5cm and |RQ| = 3cm. What is the volume of the prism?
- A. 28cm2
- B. 42cm2
- C. 70cm2
- D. 84cm2
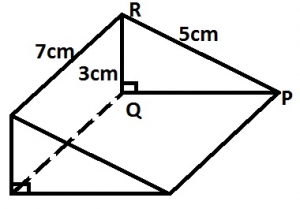
The diagram shows a triangular prism of length 7cm. The right – angled triangle PQR is a cross section of the prism |PR| = 5cm and |RQ| = 3cm. What is the area of the cross-section?
- A. 4 cm2
- B. 6cm2
- C. 15cm2
- D. 20cm2