The sides of a rectangular floor are xm and (x + 7)m. The diagonal is (x + 8)m. Calculate, in metres :
(a) the value of x ;
(b) the area of the floor.
Explanation
(a) 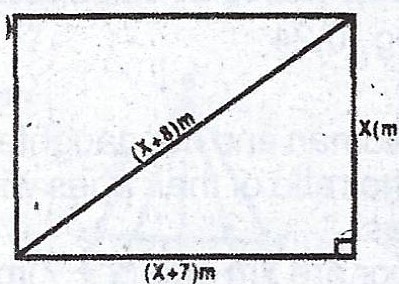
\((x + 8)^{2} = x^{2} + (x + 7)^{2}\)
\(x^{2} + 16x + 64 = x^{2} + x^{2} + 14x + 49\)
\(x^{2} + 16x + 64 - 2x^{2} - 14x - 49 = 0\)
\(15 + 2x - x^{2} = 0\)
\(x^{2} - 2x - 15 = 0\)
\((x + 3)(x - 5) = 0\)
x = 5m since measurements cannot be negative.
(b) \(Area = length \times breadth\)
Length = (x + 7) = (5 + 7) = 12 m
Breadth = x m = 5 m
\(Area = 12 \times 5 = 60 m^{2}\)

