(a) A boy blew his rubber balloon to a spherical shape. The balloon burst when its diameter was 15 cm. Calculate, correct to the nearest whole number, the volume of air in the balloon at the point of bursting. [Take \(\pi = \frac{22}{7}\)]
(b) A point X is on latitude 28°N and longitude 105°W. Y is another point on the same latitude as X but on longitude 35°E. (i) Calculate, correct to three significant figures, the distance between X and Y along latitude 28°N ; (ii) How far is X from the equator? [Take \(\pi = \frac{22}{7}\) and radius of the earth = 6,400km].
Explanation
(a) \(d = 15 cm \implies r = \frac{15}{2} cm\)
\(V = \frac{4\pi r^{3}}{3}\)
\(V = \frac{4}{3} \times \frac{22}{7} \times (\frac{15}{2})^{3}\)
\(V = \frac{1125 \times 22}{7 \times 2}\)
\(V = 1,767.857 cm^{3}\)
(b)(i)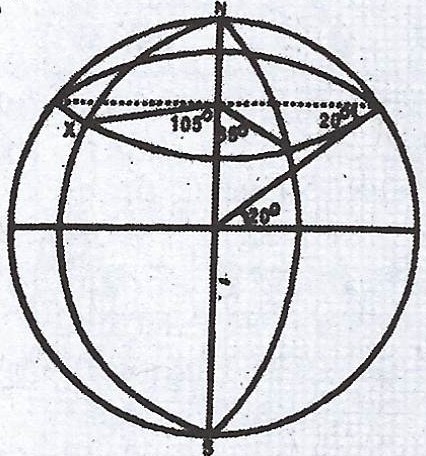 
Longitude difference : 105° + 35° = 140°
Distance along the parallel of latitude = \(\frac{140}{360} \times 2 \times \frac{22}{7} \times 6400 \cos 28\)
= \(\frac{140 \times 44 \times 6400 \times 0.8829}{360 \times 7}\)
= \(13812.48 km\)
\(\approxeq 13800 km\)
(ii) Distance from the equator : \(\frac{28}{360} \times 2 \times \frac{22}{7} \times 6400\)
= \(3128.89 km\)
\(\approxeq 3130 km\)