Mathematics JAMB, WAEC, NECO AND NABTEB Official Past Questions

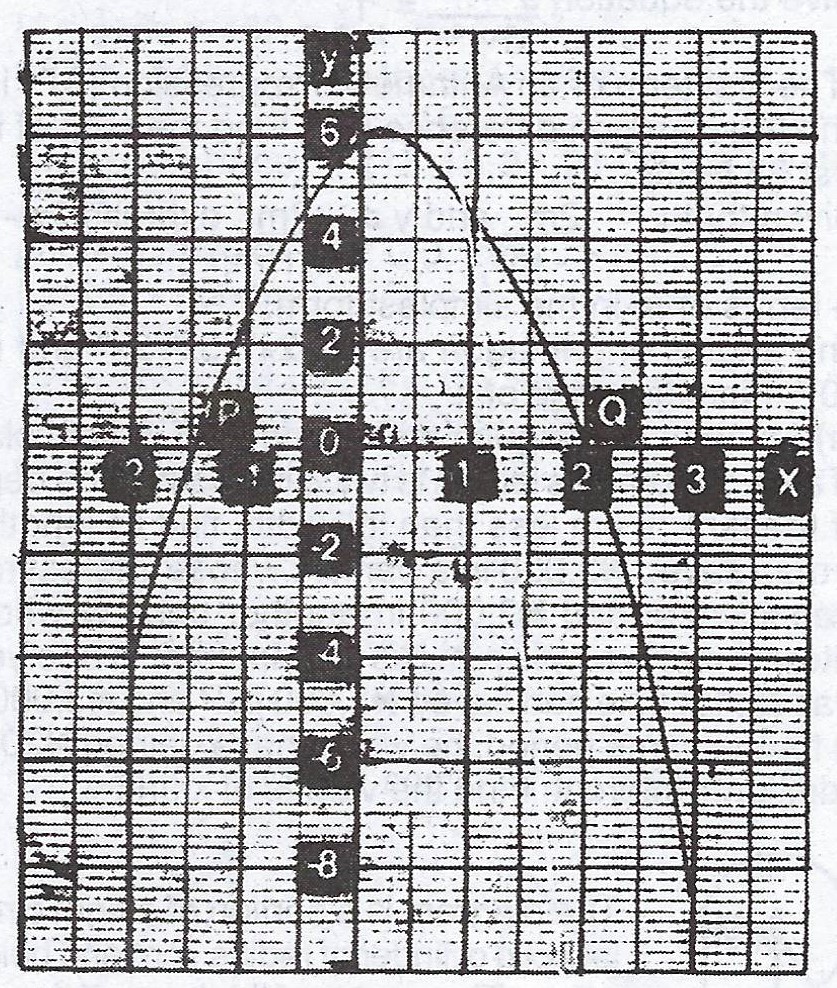
Given is the graph of the relation \(y = ax^{2} + bx + c\) where a, b and c are constants. Use the graph to :

(a) find the roots of the equation \(ax^{2} + bx + c = 0\);

(b) determine the values of constants a, b and c in the relation using the values of the coordinates P and Q and hence write down the relation illustrated in the graph

(c) find the maximum value of y and the corresponding value of x at this point.

(d) find the values of x when y = 2.

The following data gives the lengths, in cm, of 30 pieces of iron rods :

45 55 65 60 61 68 59 54 64 76 50 68 72 68 80 67 70 62 79 67 64 63 71 59 64 53 57 74 55 57

(a) Using class intervals of 45 – 49, 50 – 54, 55 – 59, … construct a frequency table of the data.

(b) Draw the histogram for the distribution

(c) Calculate the mean of the distribution

(d) What is the probability of selecting  an iron rod whose length is in the modal class?

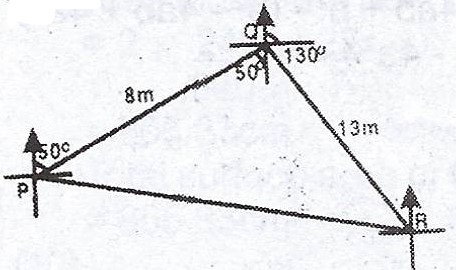In the diagram, /PQ/ = 8m, /QR/ = 13m, the bearing of Q from P is 050° and the bearing of R from Q is 130°.

(a) Calculate, correct to 3 significant figures, (i) /PR/ ; (ii) the bearing of R from P.

(b) Calculate the shortest distance between Q and PR, hence the area of triangle PQR.

Using ruler and a pair of compasses only, 

(a) construct, (i) triangle XYZ with |XY| = 8cm, < YXZ = 60° and < XYZ = 30° ; (ii) the perpendicular ZT to meet XY in T ; (iii) the locus \(l_{1}\) of points equidistant from ZY and XY.

(b) If \(l_{1}\) and ZT intersect at S, measure |ST|.

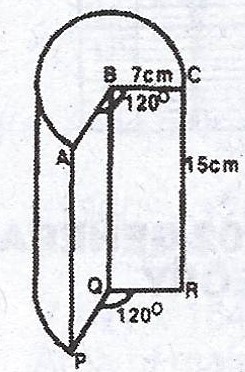 The diagram is a portion of a right circular solid cylinder of radius 7 cm and height 15 cm. The centre of the base of the cylinder is Q, while that of the top is B, where \(\stackrel\frown{ABC} = \stackrel\frown{PQR} = 120°\). Calculate, correct to one decimal place:

(a) The volume 

(b) the total surface area of the solid. [Take \(\pi = \frac{22}{7}\)].

(a) An open rectangular tank is made of a steel plate of area 1440\(m^{2}\). Its length is twice its width . If the depth of the tank is 4m less than its width, find its length.

(b) A man saved N3,000 in a bank P, whose interest rate was x% per annum and N2,000 in another bank Q whose interest rate was y% per annum. His total interest in one year was N640. If he had saved N2,000 in P and N3,000 in Q for the same period, he would have gained N20 as additional interest. Find the values of x and y.

(a) The first term of an Arithmetic Progression(AP) is 3 and the common difference is 4. Find the sum of the first 28 terms.

(b) Given that \(x = \frac{2m}{1 – m^{2}}\) and \(y = \frac{2m}{1 + m}\), express 2x – y in terms of m in the simplest form.

(c) The angles of pentagon are x°, 2x°, 3x°, 2x° and (3x – 10)°. Find the value of x.

(a) Simplify : \(\frac{1}{2}\log_{10} 25 – 2\log_{10} 3 + \log_{10} 18\)

(b) If \(123_{y} = 83_{10}\), obtain an equation in y, hence find the value of y.

(c) Solve the equation \(\frac{9^{2x – 3}}{3^{x + 3}} = 1\)

The probabilities that Ade, Kujo and Fati will pass an examination are \(\frac{2}{3}, \frac{5}{8}\) and \(\frac{3}{4}\) respectively. Find the probability that 

(a) the three ;

(b) none of them ;

(c) Ade and Kujo only ; will pass the examination.

(a) Without using calculator or mathematical tables, evaluate \(\frac{3}{\sqrt{3}}(\frac{2}{\sqrt{3}} – \frac{\sqrt{12}}{6})\)

(b) 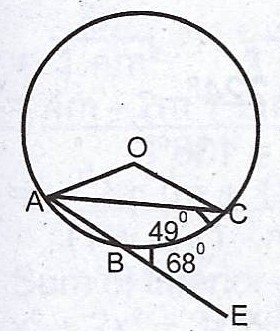 In the diagram, O is the centre of the circle. The side AB is produced to E, < ACB = 49° and < CBE = 68°. Calculate, 

(i) the interior angle AOC ; (ii) < BOC.

(a) A manufacturer offers distributors a discount of \(20%\) on any article bought and a further discount of \(2\frac{1}{2}%\) for prompt payment.

(i) if the marked price of an article is N25,000, find the total amount saved by a distributor for paying promptly. (ii) if a distributor pays N11,700 promptly for an article marked Nx, find the value of x.

(b) Factorize \(6y^{2} – 149y – 102\), hence solve the equation \(6y^{2} – 149y – 102 = 0\).

The sets A = {1, 3, 5, 7, 9, 11}, B = {2, 3, 5, 7, 11, 15} and C = {3, 6, 9, 12, 15} are subsets of \(\varepsilon\) = {1, 2, 3, …, 15}.

(a) Draw a Venn diagram to illustrate the given information.

(b) Use your diagram to find : (i) \(C \cap A’\) ; (ii) \(A’ \cap (B \cup C)\).

(a) Simplify : \((2a + b)^{2} – (b – 2a)^{2}\)

(b) Given that \(S = K\sqrt{m^{2} + n^{2}}\); (i) make m the subject of the relations ; (ii) if S = 12.2, K = 0.02 and n = 1.1, find, correct to the nearest whole number, the positive value of m.

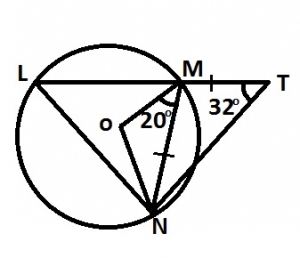
In the diagram, LMT is a straight line. lf O is the centre of circle LMN, OMN = 20°, LTN = 32° and |NM| = |MT|, find LNM.

Which of the following is not a rational number?

The number of goals scored by a school team in 10 netball matches are as follows: 3, 5, 7, 7, 8, 8, 8, 11, 11, 12. Find the probability that in a match, the school team will score at most 8 goals.

Given that \(p = x-\frac{1}{x} and\hspace{1mm}q = x^2 + \frac{1}{x^2}\) express q in terms of p.

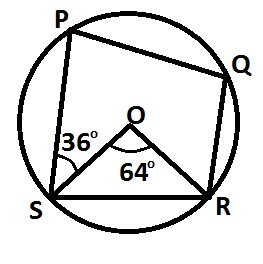
In the diagram O is the center of the circle, ∠SOR = 64° and ∠PSO = 36°. Calculate ∠PQR

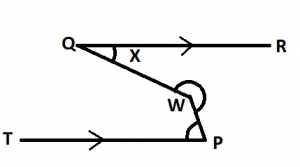
In the diagram, \(QR||TP and W\hat{P}T = 88^{\circ} \). Find the value of x

To arrive on schedule, a train is to cover a distance of 60km at 72km/hr. If it starts 10 minutes late, at what speed must it move to arrive on schedule?

Calculate and correct to two significant figures, the percentage error in approximating 0.375 to 0.4