(a) Without using calculator or mathematical tables, evaluate \(\frac{3}{\sqrt{3}}(\frac{2}{\sqrt{3}} – \frac{\sqrt{12}}{6})\)
(b)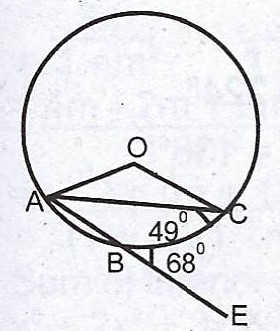 
In the diagram, O is the centre of the circle. The side AB is produced to E, < ACB = 49° and < CBE = 68°. Calculate,
(i) the interior angle AOC ; (ii) < BOC.
Explanation
(a) \(\frac{3}{\sqrt{3}}(\frac{2}{\sqrt{3}} - \frac{\sqrt{12}}{6})\)
= \(\frac{6}{\sqrt{9}} - \frac{3\sqrt{12}}{6\sqrt{3}}\)
= \(2 - \frac{2\sqrt{3}}{2\sqrt{3}}\)
= \(2 - 1 = 1\)
(b)(i) \(< ABC = 180° - 68° = 112°\)
\(< AOC = 2 \times 112° = 224°\)
\(\hat{O} = < AOC (obtuse)\)
= \(360° - 224° = 136°\)
(ii) In \(\Delta AOC\), OA = OC (radii)
\(\therefore \Delta AOC = isosceles\)
\(\hat{A} = < OAC ; \hat{C} = < ACO ; \hat{A} = \hat{C} = x\)
\(\hat{O} + \hat{A} + \hat{C} = 180°\)
\(136° + x + x = 180° \implies 2x = 44°\)
\(x = 22°\)
In \(\Delta BOC\), OB = OC (radii)
\(\therefore \Delta BOC = isosceles\)
\(< OCB = 49° + 22°= 71°\)
\(< OBC = < OCB = 71°\)
\(< OBC + < OCB + < BOC = 180°\)
\(71° + 71° + < BOC = 180°\)
\(< BOC = 180° - 142° = 38°\)