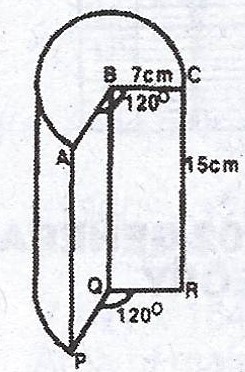
The diagram is a portion of a right circular solid cylinder of radius 7 cm and height 15 cm. The centre of the base of the cylinder is Q, while that of the top is B, where \(\stackrel\frown{ABC} = \stackrel\frown{PQR} = 120°\). Calculate, correct to one decimal place:
(a) The volume
(b) the total surface area of the solid. [Take \(\pi = \frac{22}{7}\)].
Explanation
(a) Area of the major sector = \(\frac{\theta}{360°} \times \pi r^{2}\)
= \(\frac{360 - 120}{360} \times \frac{22}{7} \times 7 \times 7\)
= \((\frac{2}{3} \times 154) cm^{2}\)
Volume = \(\text{Area of the major sector} \times \text{height (cross section)}\)
= \(\frac{2}{3} \times 154 \times 15 = 1540 cm^{3}\)
(b) Curved surface area = \(\frac{240}{360} \times 2\pi rh\)
= \(\frac{240}{360} \times 2 \times \frac{22}{7} \times 7 \times 15\)
= \(440 cm^{2}\)
Area of rectangular surface = \(2 \times l \times b\)
= \(2 \times 7 \times 15 = 210 cm^{2}\)
Area of top and bottom of cylinder (major sector)
= \(2 \times \frac{240}{360} \times \frac{22}{7} \times 7 \times 7\)
= \(205.33 cm^{2}\)
\(\therefore \text{Total surface area} = 440 + 205.33 + 210 = 855.33 cm^{2}\)