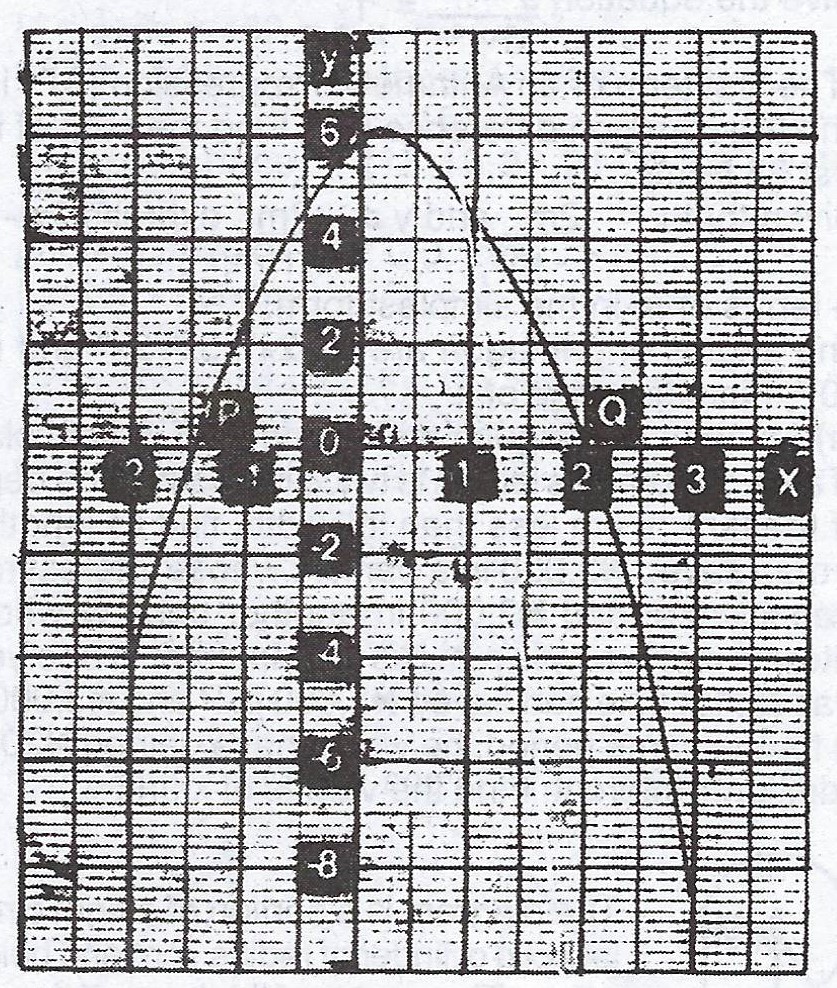
Given is the graph of the relation \(y = ax^{2} + bx + c\) where a, b and c are constants. Use the graph to :
(a) find the roots of the equation \(ax^{2} + bx + c = 0\);
(b) determine the values of constants a, b and c in the relation using the values of the coordinates P and Q and hence write down the relation illustrated in the graph
(c) find the maximum value of y and the corresponding value of x at this point.
(d) find the values of x when y = 2.
Explanation
(a) The roots of the equation are -1.5 or 2.
(b) C = 6 (intercept on the positive vertical axis)
\(ax^{2} + bx + c = 0\)
When x = 2, c = 6
\(4a + 2b + 6 = 0 \implies 4a + 2b = -6 ....(1)\)
When x = -1.5, c = 6
\(a(-1.5)^{2} + b(-1.5) = -6\)
\(\frac{9a}{4} - \frac{3b}{2} = -6 \implies 9a - 6b = -24 ... (2)\)
Multiply (1) by 3 : \(12a + 6b = -18 ... (1a)\)
(1a) + (2) : \(12a + 9a = -18 - 24 \implies 21a = -42\)
\(a = -2\)
\(4a + 2b = -6 \implies 4(-2) + 2b = -6\)
\(2b = -6 + 8 = 2 \implies b = 1\)
(a, b, c) = (-2, 1, 6)
Hence the relation illustrated in the graph is \(y = -2x^{2} + x + 6\).
(c) When \(x = 0.2, y_{max} = 6.2\)
(d) When \(y = 2, x = \text{ -1.2 or 1.7}\)

