The table below shows the values of the relation \(y = 11 – 2x – 2x^{2}\) for \(-4 \leq x \leq 3\).
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -13 | 11 |
(a) Copy and complete the table.
(b) Using a scale of 2 cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of \(y = 11 – 2x – 2x^{2}\).
(c) Use your graph to find : (i) the roots of the equation \(11 – 2x – 2x^{2} = 0\) ; (ii) the values of x for which \(3 – 2x – 2x^{2} = 0\) ; (iii) the gradient of the curve at x = 1.
Using ruler and a pair of compasses only,
(a) construct a quadrilateral PXYQ such that /PX/ = 9.9 cm, /QX/ = 10.2 cm, < QPZ = 75°, /QY/ = 10.4 cm and PQ // XY.
(b) Construct the (i) locus \(l_{1}\) of points equidistant from X and Y ; (ii) locus \(l_{2}\) of points equidistant from QY and YX.
(c) Locate M, the point of intersection of \(l_{1}\) and \(l_{2}\).
(d) Measure /PM/.
An aeroplane flies due west for 3 hours from P (lat. 50°N, long. 60°W) to a point Q at an average speed of 600km/h. The aeroplane then flies due south from Q to a point Y 500km away. Calculate, correct to 3 significant figures,
(a) the longitude of Q ;
(b) the latitude of Y . [Take the radius of the earth = 6400km and \(\pi = \frac{22}{7}\)].
In the diagram, PQT is a straight line and SQ // RT.
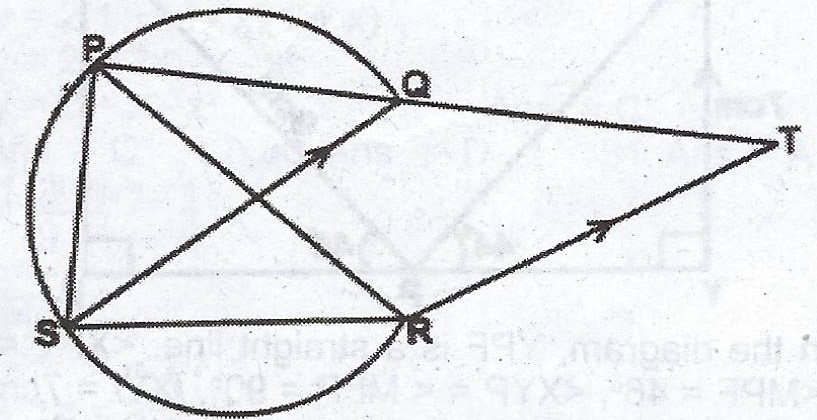
(a) Join QR and show that : (i) < RPS = < QRT ; (ii) < PRS = < QTR.
(b) ABC is a triangle. The sides AB and AC are produced to D and E respectively such that < DBC = 132° and < ECD = 96°. Show that \(\Delta\) ABC is isosceles.
The marks obtained by 40 students in an examination are as follows :
85 77 87 74 77 78 79 89 95 90 78 73 86 83 91 74 84 81 83 75 77 70 81 69 75 63 76 87 61 78 69 96 65 80 84 80 77 74 88 72.
(a) Copy and complete the table for the distribution using the above data.
| Class Boundaries | Tally | Frequency |
| 59.5 – 64.5 | ||
| 64.5 – 69.5 | ||
| 69.5 – 74.5 | ||
| 74.5 – 79.5 | ||
| 79.5 – 84.5 | ||
| 84.5 – 89.5 | ||
| 89.5 – 94.5 | ||
| 94.5 – 99.5 |
(b) Draw a histogram to represent the distribution.
(c) Using your histogram, estimate the modal mark.
(d) If a student is chosen at random, find the probability that the student obtains a mark greater than 79.
(a) A = {1, 2, 5, 7} and B = {1, 3, 6, 7} are subsets of the universal set U = {1, 2, 3,…., 10}. Find (i) \(A’\) ; (ii) \((A \cap B)’\) ; (iii) \((A \cup B)’\) ; (iv) the subsets of B each of which has three elements.
(b) Write down the 15th term of the sequence, \(\frac{2}{1 \times 3}, \frac{2}{2 \times 4}, \frac{4}{3 \times 5}, \frac{5}{4 \times 6},…\).
(c) An Arithmetic Progression (A.P) has 3 as its first term and 4 as the common difference, (i) write an expression in its simplest form for the nth term ; (ii) find the least term of the A.P that is greater than 100.
The table shows the monthly contributions and expenditure pattern of an employee in 1999.
| Item | Percentage |
| Pension | 5 |
| Income Tax | 25 |
| Food | 40 |
| Transport | 10 |
| Rent | 12.5 |
| Others | 7.5 |
(a) Draw a pie chart to illustrate the data.
(b) If the employee’s gross monthly salary was N10,800.00, calculate (i) the pension contribution of the employee ; (ii) the income tax paid by the employee.
(c) If the pension contribution and income tax were deducted from the gross monthly salary, before payment, calculate the take- home pay of the employee.
(a) Simplify : \(\frac{\frac{1}{3}c^{2} – \frac{2}{3}cd}{\frac{1}{2}d^{2} – \frac{1}{4}cd}\)
(b) 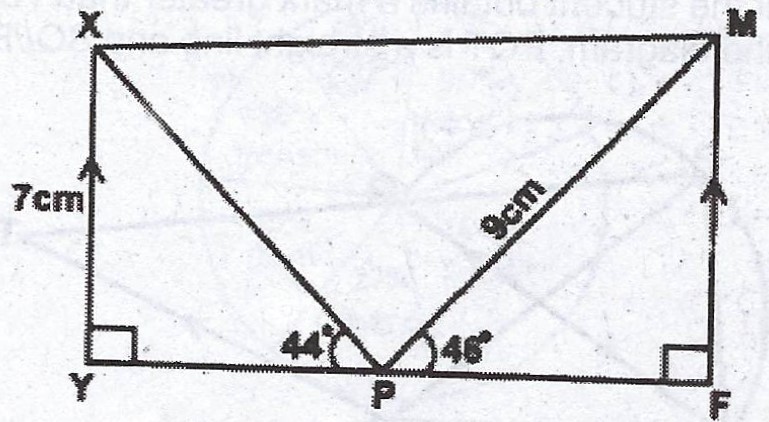
In the diagram, YPF is a straight line. < XPY = 44°, < MPF = 46°, < XYP = < MFP = 90°, /XY/ = 7cm and /MP/ = 9 cm.
(i) Calculate, correct to 3 significant figures, /XM/ and /YF/ ; (ii) Find < XMP.
The table shows the number of suitcases possessed by a group of travellers.
| No. of suitcases | 0 | 1 | 2 | 3 | 4 | 5 |
| Travellers | 2 | 7 | 7 | 2 | 3 | 9 |
(a) Calculate the (i) median (ii) mean, correct to the nearest whole number.
(b) Draw a bar chart to represent the information.
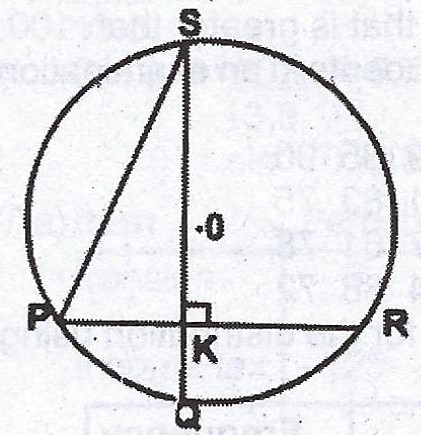 In the diagram, PQRS is a circle with centre O and radius 7cm. SQ and PR intersect at K and < SKR = 90°. If the length of the arc SR is four times that of arc PQ, find the length of the arc SR. [Take \(\pi = \frac{22}{7}\)].
In the diagram, PQRS is a circle with centre O and radius 7cm. SQ and PR intersect at K and < SKR = 90°. If the length of the arc SR is four times that of arc PQ, find the length of the arc SR. [Take \(\pi = \frac{22}{7}\)].
(a) Simplify : \(625^{\frac{3}{8}} \times 5^{\frac{1}{2}} \div 25\)
(b) Solve the following equations correct to one decimal place.
(i) \(\tan (\theta + 25)° = 5.145\)
(ii) \(5\cos \theta – 1 = 0\), where \(0° \leq \theta \leq 90°\).
Without using Mathematical tables or a calculator, simplify :
(a) \(\sqrt{50} – 3\sqrt{2}(2\sqrt{2} – 5) – 5\sqrt{32}\)
(b) \(\frac{1}{2} \log_{10} \frac{25}{4} – 2 \log_{10} \frac{4}{5} + \log_{10} \frac{320}{125}\).
(a) If p varies directly as \(r^{2}\) and p = 3.2 when r = 4, find the value of p when r = 6.5.
(b) Solve the simultaneous equations :
\(\frac{x}{2} + \frac{y}{4} = 1 ; \frac{x}{3} – \frac{y}{4} = \frac{-1}{6}\)
Which of the following is not a measure of dispersion?
- A. Range
- B. Mean deviation
- C. Mean
- D. Standard deviation
The bearing of P from Q is x, where 270o < x < 360o. Find the bearing of Q from P
- A. (x - 90)o
- B. (x-270)o
- C. (x - 135)o
- D. (x - 180)o
A man made a loss of 15% by selling an article for N595. Find the cost price of the article
- A. N600.00
- B. N684.25
- C. N700.00
- D. N892.50
A right circular cone is such that its radius r is twice its height h. Find its volume in terms of h
- A. \(\frac{2}{3}\pi h^2\)
- B. \(\frac{1}{12}\pi h^3\)
- C. \(\frac{4}{3}\pi h^2\)
- D. \(\frac{4}{3}\pi h^3\)
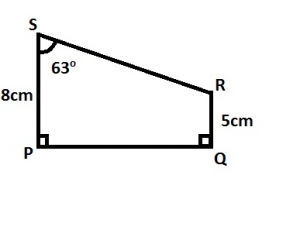
In the diagram /PS/ = 9 cm, /OR/ = 5cm, \(P\hat{S}R = 63^o\) and \(S\hat{P}Q = P\hat{Q}R = 90^o\). Find, correct to the nearest whole number, the area of the trapezium,
- A. 55cm2
- B. 25cm2
- C. 22cm2
- D. 13cm2
In constructing an angle, Olu draws line OX. With centre O and a convenient radius, he draws an arc intersecting OX at P. With centre P and the same radius, he draws an arc intersecting the first arc at Q and finally joins OQ. What is the size of angle POQ so constructed?
- A. 90o
- B. 75o
- C. 60o
- D. 45o
Evaluate Cos 45o Cos 30o – Sin 45o Sin 30o leaving the answer in surd form
- A. \(\frac{\sqrt{2}-1}{2}\)
- B. \(\frac{\sqrt{3}-\sqrt{2}}{4}\)
- C. \(\frac{\sqrt{6}-\sqrt{2}}{2}\)
- D. \(\frac{\sqrt{6}-\sqrt{2}}{4}\)
Find the equation whose roots are \(-\frac{2}{3}\) and 3
- A. 3x2+11x-6=0
- B. 3x2+7x+6=0
- C. 3x2-11x-6=0
- D. 3x2-7x-6=0


