The locus of points equidistant from two intersecting straight lines PQ and PR is
- A. a circle centre P radius Q.
- B. a circle centre P radius PR
- C. the point of intersection of the perpendicular bisectors of PQ and PR
- D. the bisector of angle QPR
The probabilities of a boy passing English and Mathematics test are x and y respectively. Find the probability of the boy failing both tests
- A. 1-(x-y)+xy
- B. 1-(x+y)-xy
- C. 1-(x+y)+xy
- D. 1 - (x - y) + x
Given that p varies as the square of q and q varies inversely as the square root of r. How does p vary with r?
- A. p varies as the square of r
- B. p varies as the square root of r
- C. p varies inversely as the square of r
- D. p varies inversely as r
The square root of a number is 2k. What is half of the number
- A. \(\sqrt{\frac{k}{2}}\)
- B. \(\sqrt{k}\)
- C. \(\frac{1}{2}k^2\)
- D. 2k2
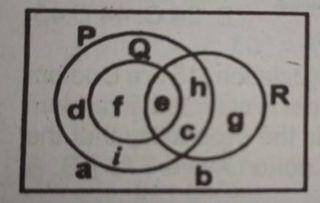
From the Venn Diagram below, find Q’ ∩ R.
- A. (e)
- B. (c, h)
- C. (c, g, h)
- D. (c, e, g, h)
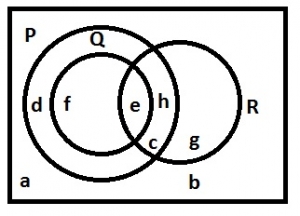
From the Venn diagram below, how many elements are in P∩Q?
- A. 1
- B. 2
- C. 4
- D. 6
If \(P = \sqrt{QR\left(1+\frac{3t}{R}\right)}\), make R the subject of the formula.
- A. \(R = \frac{3Qt}{P^2 - Q}\)
- B. \(R = \frac{P^2 – 3t}{Q+1}\)
- C. \(R = \frac{P^2 + 3t}{Q - 1}\)
- D. \(R = \frac{P^2-3Qt}{Q}\)
In a ∆ XYZ, /YZ/ = 6cm YXZ = 60o and XYZ is a right angle. Calculate /XZ/in cm, leaving your answer in surd form
- A. 2√3
- B. 4√3
- C. 6√3
- D. 12√3
Which of the following is/are not the interior angle(s) of a regular polygon? I.108° II. 116° III. 120°
- A. I only
- B. II only
- C. III only
- D. I and III only
If \(\frac{3^{(1-n)}}{9^{-2n}}=\frac{1}{9}\) find n
- A. \(-\frac{3}{2}\)
- B. \(\frac{1}{3}\)
- C. -1
- D. -3
Given that x ≅ 0.0102 correct to 3 significant figures, which of the following cannot be the actual value of x?
- A. 0.01014
- B. 0.01021
- C. 0.01015
- D. 0.01016
Evaluate \((111_{two})^2 – (101_{two})^2\)
- A. 10two
- B. 100two
- C. 1100two
- D. 11000two
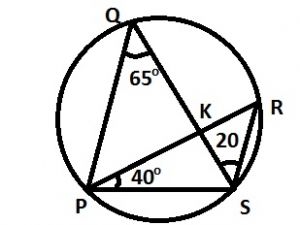
In the diagram, \(P\hat{Q}S = 65^o, R\hat{P}S = 40^o\hspace{1mm}and\hspace{1mm}Q\hat{S}R=20^o\hspace{1mm} Find P\hat{S}Q\)
- A. 85o
- B. 60o
- C. 55o
- D. 45o
Find the values of x for which \( \frac{1}{2x^2 – 13x +15} \) is not defined,
- A. 5 or \( \frac{3}{2} \)
- B. 1 or \( \frac{15}{13} \)
- C. 2 or 15
- D. 13 or 15
Out of 60 members of an Association, 15 are Doctors and 9 are Lawyers. If a member is selected at random from the Association, what is the probability that the member is neither a Doctor Nor a Lawyer
- A. \(\frac{3}{5}\)
- B. \(\frac{9}{10}\)
- C. \(\frac{3}{20}\)
- D. \(\frac{1}{4}\)
The four interior angles of a quadrilateral are (x + 20) o, (x+ 10) o (2x – 45) o and (x – 25) o. Find the value of x
- A. 60
- B. 80
- C. 100
- D. 360
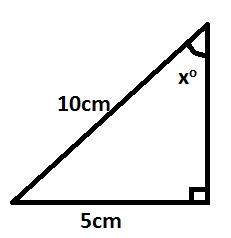
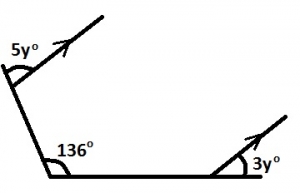
What is the size of angle x in the diagram
- A. 15o
- B. 30o
- C. 45o
- D. 60o
A ladder, 6m long, leans against a vertical wall at an angle 53o to the horizontal. How high up the wall does the ladder reach?
- A. 3.611m
- B. 4.521m
- C. 4.792m
- D. 7.962m
Given, that \(4P4_5 = 119_{10}\), find the value of P
- A. 1
- B. 2
- C. 3
- D. 4
In\( ∆ PQR, P\hat{Q}P = 84^°, |Q\hat{P}R |= 43^°\) and |PQ| = 5cm. Find /QR/ in cm, correct to 1 decimal place.
- A. 3.4
- B. 4.3
- C. 5.9
- D. 6.2