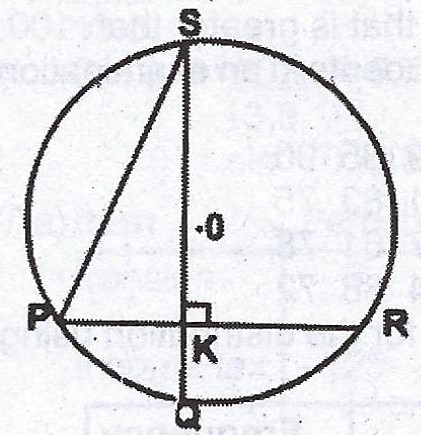
In the diagram, PQRS is a circle with centre O and radius 7cm. SQ and PR intersect at K and < SKR = 90°. If the length of the arc SR is four times that of arc PQ, find the length of the arc SR. [Take \(\pi = \frac{22}{7}\)].
Explanation
Let < POQ = \(\theta\)
\(\implies\) SR = \(4\theta\).
\(< PSQ = \frac{\theta}{2} ; < SPR = 2\theta\)
In \(\Delta PSK\),
\(2\theta + \frac{\theta}{2} = 90°\)
\(\frac{5\theta}{2} = 90° \implies 5\theta = 180°\)
\(\theta = \frac{180°}{5} = 36°\)
\(\therefore < SOR = 4\theta = 4 \times 36° = 144°\)
Length of arc = \(\frac{\theta}{360°} \times 2\pi r\)
\(\frac{144}{360} \times 2 \times \frac{22}{7} \times 7 \)
= \(17.6 cm\).