In the diagram, PQT is a straight line and SQ // RT.
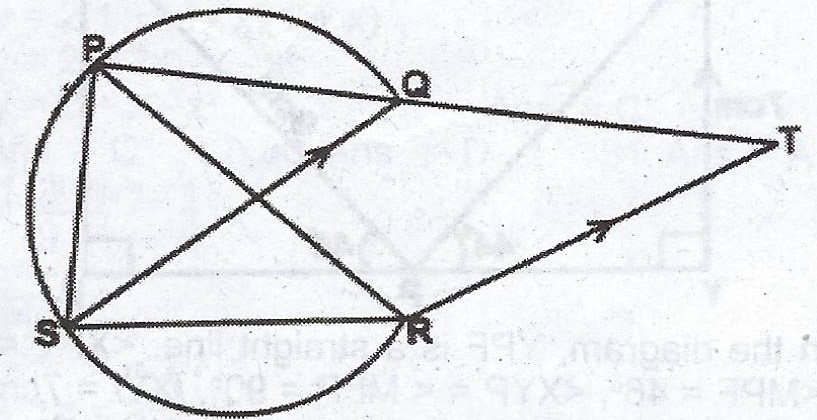
(a) Join QR and show that : (i) < RPS = < QRT ; (ii) < PRS = < QTR.
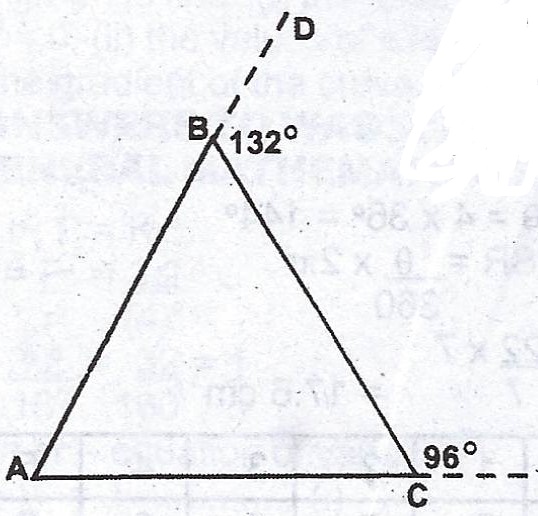
(b) ABC is a triangle. The sides AB and AC are produced to D and E respectively such that < DBC = 132° and < ECD = 96°. Show that \(\Delta\) ABC is isosceles.
Explanation
(a) < QRT = < RQS (alternate angles)
< RPS = < RQS (angles in the same segment)
\(\therefore\) < RPS = < QRT
(ii) < QRT = < PQS (corresponding angles)
< PQS = < PRS (angles in the same segment)
\(\therefore\) < QTR = < PRS.
(b) \(< ABC = \hat{B} = 180° - 132° = 48°\)
\(< ACB = \hat{C} = 180° - 96° = 84°\)
\(< BAC = \hat{A} = 180° - (48° + 84°) = 48°\)
\(< BAC = < ABC = 48°\)
\(\therefore \Delta ABC = isosceles\).