An aeroplane flies due west for 3 hours from P (lat. 50°N, long. 60°W) to a point Q at an average speed of 600km/h. The aeroplane then flies due south from Q to a point Y 500km away. Calculate, correct to 3 significant figures,
(a) the longitude of Q ;
(b) the latitude of Y . [Take the radius of the earth = 6400km and \(\pi = \frac{22}{7}\)].
Explanation
(a) 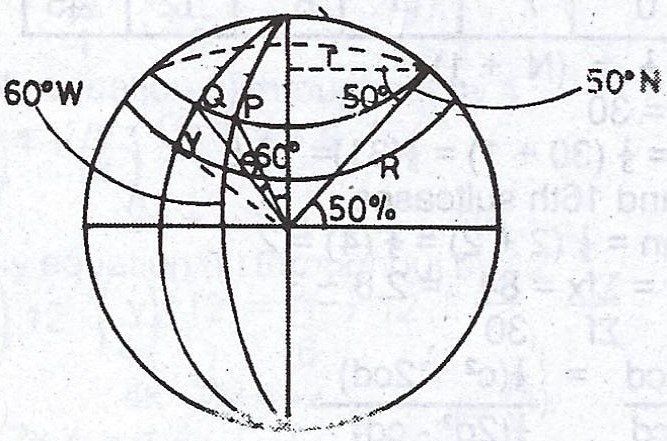
\(\frac{r}{R} = \cos 50\)
\(r = 6400 \cos 50 = 4,113.84 km\)
\(\approxeq 4,114km\)
The distance PQ along the parallel of latitude = speed (km/h) \(\times\) time (h)
= 600km/h x 3h
= 1800km
\(\frac{\theta}{360} \times 2 \times \frac{22}{7} \times r = 1800\)
\(\theta = \frac{1800 \times 7 \times 360}{44 \times 4113.84}\)
\(\theta = 25.059° \approxeq 25.1°\)
\(\therefore\) The longitude of Q = \(60 + \theta\)
= \(60 + 25.1 = 85.1°W\)
(b) The distance (Q) along the meridian
\(\frac{\theta}{360} \times 2\pi R\)
\(500 = \frac{\theta}{360} \times 2 \times \frac{22}{7} \times 6400\)
\(\theta = \frac{500 \times 360 \times 7}{44 \times 6400}\)
\(\theta = 4.47°\)
\(\therefore \text{The latitude of Y} = 50° - 4.47° = 45.53°\)
\(\approxeq 45.5°N\)

