(a) Copy and complete the following table of values for the relation \(y = 2x^{2} – 7x – 3\).
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 19 | -3 | -9 |
(b) Using 2 cm to 1 unit on the x- axis and 2 cm to 5 units on the y- axis, draw the graph of \(y = 2x^{2} – 7x – 3\) for \(-2 \leq x \leq 5\).
(c) From your graph, find the : (i) minimum value of y ;
(ii) gradient of the curve at x = 1.
(d) By drawing a suitable straight line, find the values of x for which \(2x^{2} – 7x – 5 = x + 4\).
(a) Simplify : \(\sqrt{1001_{two}}\), leaving your answer in base two.
(b) 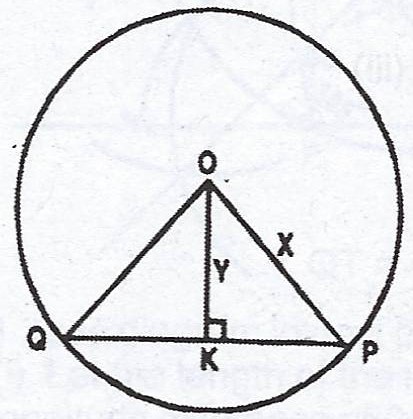
In the diagram, O is the centre of the circle radius x. /PQ/ = z, /OK/ = y and < OKP = 90°. Find the value of z in terms of x and y.
(c) 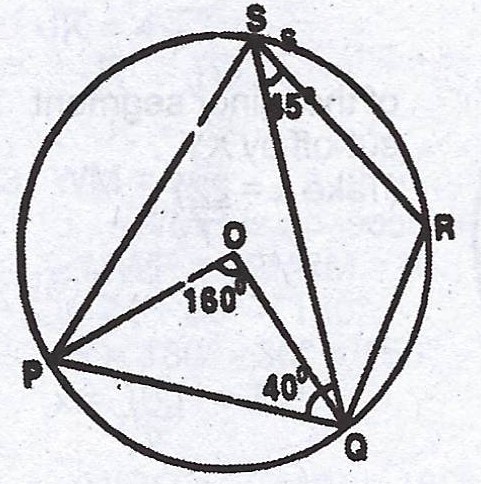
In the diagram, P, Q, R and S are points of the circle centre O. \(\stackrel\frown{POQ} = 160°\), \(\stackrel\frown{QSR} = 45°\) and \(\stackrel\frown{PQS} = 40°\). Calculate, (i) < QPS ; (ii) < RQS.
The frequency distribution shows tha marks of 100 students in a Mathematics test.
| Marks | 1-10 | 11-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 | 81-90 | 91-100 |
|
No. of Students |
2 | 4 | 9 | 13 | 18 | 32 | 13 | 5 | 3 | 1 |
(a) Draw cumulative frequency curve for the distribution .
(b) Use your curve to estimate : (i) the median ; (ii) the lower quartile ; (iii) the 60th percentile.
K(lat. 60°N, long. 50°W) is a point on the eart’s surface. L is another point due East of K and the third point N is due South of K. The distance KL is 3520km and KN is 10951km.
(a) Calculate: (i) The longitude of L ; (ii) The latitude of N. (Take \(\pi = \frac{22}{7}\) and the radius of the earth = 6400km).
(b) A man was allowed 20% of his income as tax free. He then paid 25 kobo in the naira on the remainder. If he paid N1,200.00 as tax, calculate his total income.
Using a ruler and a pair of compasses only,
(a) Construct : (i) \(\Delta PQR\) such that /PQ/ = 8cm, /PR/ = 7cm and < QPR = 105°. (ii) locus \(L_{1}\) of points equidistant from P and Q. (iii) locus \(l_{2}\) of points equidistant Q and R.
(b)(i) Label the point T where \(l_{1}\) and \(l_{2}\) intersect ; (ii) With centre T and radius /TQ/, construct a circle \(l_{3}\). (iii) Complete quadrilateral PQSR such that /RS/ = /QS/ and /RQ/ = /TS/.
(a) 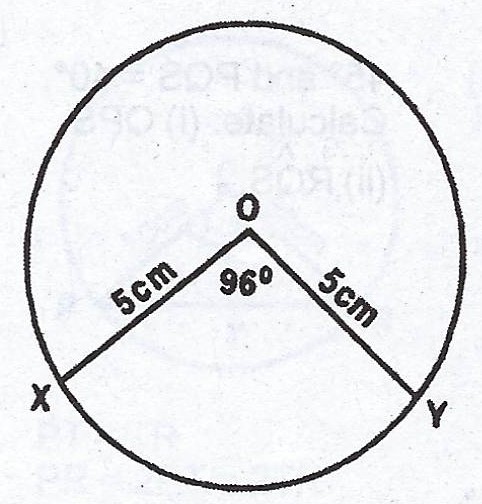
In the diagram, XY is a chord of a circle of radius 5cm. The chord subtends an angle 96° at the centre. Calculate, correct to three significant figures, the area of the minor segment cut-off. (Take \(\pi = \frac{22}{7}\)).
(b) 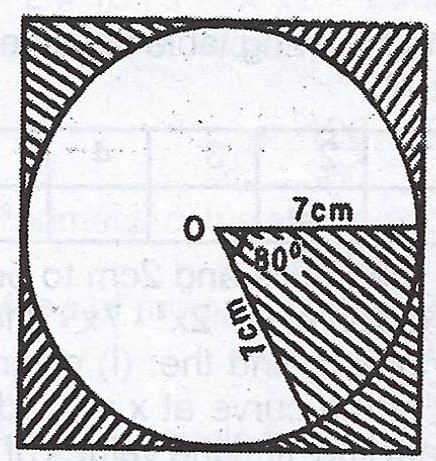 The figure shows a circle inscribed in a square. If a portion of the circle is shaded with some portions of the square, calculate the total area of the shaded portions. [Take \(\pi = \frac{22}{7}\)].
The figure shows a circle inscribed in a square. If a portion of the circle is shaded with some portions of the square, calculate the total area of the shaded portions. [Take \(\pi = \frac{22}{7}\)].
(a) The angles of depression of the top and bottom of a building are 51° and 62° respectively from the top of a tower 72m high. The base of the building is on the same horizontal level as the foot of the tower. Calculate the height of the building correct to 2 significant figures.
(b) 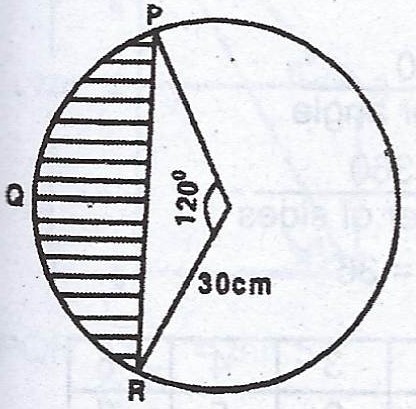 In the diagram, PR is a chord of the circle centre O and radius 30cm, < POR = 120°. Calculate correct to three significant figures : (i) the length of chord PR ; (ii) the length of arc PQR ; (iii) the perimeter of the shaded portion. (Take \(\pi = 3.142\)).
In the diagram, PR is a chord of the circle centre O and radius 30cm, < POR = 120°. Calculate correct to three significant figures : (i) the length of chord PR ; (ii) the length of arc PQR ; (iii) the perimeter of the shaded portion. (Take \(\pi = 3.142\)).
(a) Simplify : \((\frac{x^{2}}{2} – x + \frac{1}{2})(\frac{1}{x – 1})\)
(b) A point P is 40km from Q on a bearing 061°. Calculate, correct to one decimal place, the distance of P to (i) north of Q ; (ii) east of Q.
(c) A man left N5,720 to be shared among his son and three daughters. Each daughter’s share was \(\frac{3}{4}\) of the son’s share. How much did the son receive?
The table shows the marks scored by a group of students in a class test.
| Marks | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 4 | 9 | 8 | 5 | 3 |
(a)(i) Calculate the mean mark ; (ii) Find the median.
(b) If the information were to be represented in a pie chart, what would be the sectorial angle for the mark 2?
(a) The sides of an isosceles triangle triangle are in the ratio \(7 : 5 : 7\). Calculate, correct to the nearest degree, the angle included between the equal sides.
(b) The sum of the interior angles of a regular polygon is 1440°. Calculate : (i) the number of sides ; (ii) the size of one exterior angle of the polygon.
(a) AB is a chord of a circle centre O. If |AB| = 24.2 cm and the perimeter of \(\Delta\) AOB is 52.2 cm, calculate < AOB, correct to the nearest degree.
(b) A rectangular tank 60cm by 80cm by 100cm is half filled with water. How many litres of water is it holding?
(a) In the simultaneous equations : \(px + qy = 5 ; qx + py = -10\); p and q are constants. If x = 1 and y = -2 is a solution of the equations, find p and q.
(b) Solve : \(\frac{4r – 3}{6r + 1} = \frac{2r – 1}{3r + 4}\).
(a) Solve \(\frac{1}{81^{(x – 2)}} = 27^{(1 – x)}\)
(b) Simplify \(\frac{5}{\sqrt{7} – \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{3}}\), leaving your answer in surd form.
A point on the ground is 5m away from the foot of a vertical wall 7 m high, Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall
- A. 36o
- B. 44o
- C. 46o
- D. 54o
A bag contains 3 red and 2 white identical balls. lf 2 balls are picked at random from the bag, one after the other and with replacement, find the probability that they are of different colours
- A. \(\frac{36}{625}\)
- B. \(\frac{16}{625}\)
- C. \(\frac{12}{25}\)
- D. \(\frac{13}{25}\)
A Cooperative Society, charges an interest of 51/2% per annum on any amount borrowed by its members. If a member borrows N125,000, how much does he pay back after one year?
- A. N136875
- B. N131,875
- C. N126750
- D. N126250
Given that p = 2, q = -5 and r = – 4, evaluate 3p2 – q2 – r3
- A. 101
- B. 77
- C. 51
- D. -27
The sides of two cubes are in the ratio 2:5. What is the ratio of their volumes?
- A. 4:5
- B. 8: 15
- C. 6:125
- D. 8:125
Which of the following is/are true? In a plane, the locus of points I. Equidistant from a straight line is a circle radius d where d is the distance between the point and the straight line.
II Equidistant from two given points P and Q is a circle of radius |PQ|. III Equidistant from two points is the perpendicular bisector of the line joining the two points.
- A. I only
- B. II only
- C. III only
- D. I, II and III
Given that \(P\propto \frac{1}{\sqrt{r}}\) and p = 3 when r = 16, find the value of r when p = 3/2
- A. 48
- B. 64
- C. 72
- D. 324
The locus of a point which moves in a plane such that it is equidistant from two fixed points X and Y is
- A. the perpendicular bisector of the line segment X Y
- B. a line parallel to the line segment XY
- C. a circle with XY as diameter
- D. the line perpendicular to the line segment XY


