(a) The sides of an isosceles triangle triangle are in the ratio \(7 : 5 : 7\). Calculate, correct to the nearest degree, the angle included between the equal sides.
(b) The sum of the interior angles of a regular polygon is 1440°. Calculate : (i) the number of sides ; (ii) the size of one exterior angle of the polygon.
Explanation
(a) 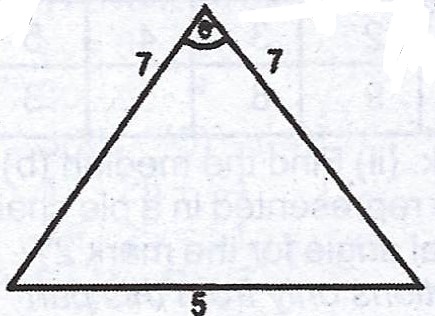
\(5^{2} = 7^{2} + 7^{2} - 2(7)(7) \cos \theta\)
\(25 = 98 - 98 \cos \theta\)
\(\cos \theta = \frac{98 - 25}{98}\)
\(\cos \theta = 0.7449\)
\(\theta = \cos^{-1} (0.7449)\)
\(\approxeq 42°\).
(b) (i) \((2n - 4) \times 90° = 1440°\)
\(2n - 4 = \frac{1440}{90} = 16\)
\(2n = 16 + 4 = 20\)
\(n = 10\)
(ii) Size of exterior angle = \(\frac{360}{\text{Number of sides}}\)
= \(\frac{360}{10}\)
= \(36°\)

